最优化 - 信赖域和直接搜索
Trust Region Methods 信赖域方法
- Problem Description 问题描述
- Optimality Conditions 最优化条件
- Line Search Methods 线搜索方法
- Trust Region Methods 信赖域方法
- Direct Search Methods 直接搜索法
- Nonlinear Least Squares(NLS) 非线性最小二乘法 – LMA
文章目录
- Trust Region Methods 信赖域方法
- 信赖域算法介绍
- 数学模型
- 信赖域算法流程
- [关于子问题的最优解]
- ⭕折线算法 Dog-Leg Method
- 定义完全步(Full Step)
- 折线算法
- Direct Search Methods 直接搜索法
- 介绍
- 1. Box Search
- 2. Section 坐标搜索算法 (属于线搜索算法)
- 3. ⭕Nelder Mead
- 1. reflection
- 2. Explansion
- 3. outer contraction
- 4. inner contraction
- 5. shinking
- 总结 Nelder Mead 算法流程:
- Nonlinear Least Squares(NLS) 非线性最小二乘法 -- LMA
- 一
- 二:问题定义
- 三:问题的解
- 非约束优化总结
- 线搜索&信赖域
- 直接搜索
- 直接搜索
信赖域算法介绍
最优化的目标是找到极小值点,在这个过程中,我们需要从一个初始点开始,先确定一个搜索方向 p ,在这个方向上做线搜索(line search),找到此方向上的可接受点(例如,按两个准则的判定)之后,通过一定的策略调整搜索方向,然后继续在新的方向上进行一维搜索,依此类推,直到我们认为目标函数已经收敛到了极小值点。
信赖域算法与一维搜索算法的区别、联系
在Jorge Nocedal和Stephen J. Wright的《Numerical Optimization》一书的第2.2节介绍了解优化问题的两种策略-line search和trust region。本质上它们的作用都是在优化迭代过程中从当前点找寻下一点。它们的最大区别是先确定步长还是先确定方向。
-
信赖域方法与线搜索算法不同之处其一在于, 后者先产生搜索方向p‾(k)\underline p^{(k)}p(k), 再求一合适的步长α(k)\alpha^{(k)}α(k), 迭代依照的如下形式进行
-
θ‾(k+1)=θ‾(k)+α(k)p‾(k)\underline\theta^{(k+1)} =\underline\theta^{(k)}+\alpha^{(k)} \underline p^{(k)} θ(k+1)=θ(k)+α(k)p(k)
-
而trust region方法则先把搜索范围缩小到一个小的范围,小到能够用另一个函数(Model function)去近似目标函数(Objective function),然后通过优化这个model function来得到参数更新的方向及步长。
同时选取搜索方向与步长 (或者说, 先划定步长的范围, 再选取搜索方向) . 迭代的方式为 $\underline\theta^{(k+1)} =\underline\theta^{(k)}+ \underline p^{(k)} $ (可以认为此时步长融于p‾(k)\underline p^{(k)}p(k) 中)
线搜索方法用得比信赖域方法广泛,是不是说明信赖域方法没有优点呢?
举个简单的例子,求解:
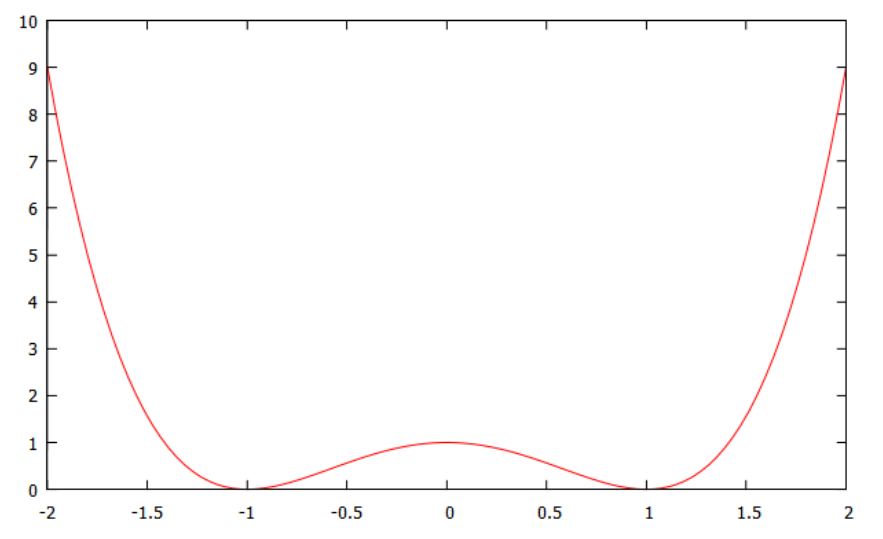
如果直接用线搜索,初始点在 0 处无法进行下一步的搜索,因为梯度为0. 而使用TR:,显然可以往最优方向进行搜索。
https://blog.csdn.net/purgle/article/details/73800186
信赖域算法的基本思想
下面是线搜索算法与信赖域算法的一个图例.
- 图中, 椭圆虚线为建立的模型(model function) m(k)m^{(k)}m(k) 的等高线, 而圆形虚线为信赖域的边界.
- 从图中可以看到, 线搜索得到的函数值下降并不客观 (当然这可能与 m(k)m^{(k)}m(k) 对目标函数的近似程度有关) ,
- 而信赖域方法得到的下一迭代点被牢牢地锁在信赖域中, 反而带来了较大的下降.
trust region方法则先把搜索范围缩小到一个小的范围,小到能够用另一个函数(Model function)去近似目标函数(Objective function),然后通过优化这个model function来得到参数更新的方向及步长。
由上面的表述我们可以得到信赖域方法的几个要素
- 近似模型函数 m(k)(p‾)m^{(k)}(\underline p)m(k)(p)
- 可信赖域 region of trust TΔ\mathcal T_\DeltaTΔ
- 迭代增量 p‾\underline pp (包括步长和方向)
-
近似目标函数的 model fuction 为:
J(θ‾(k))≈m(k)(0‾)J(\underline\theta^{(k)}) \approx m^{(k)}(\underline 0) J(θ(k))≈m(k)(0) -
代替最小化目标函数,TR 方法最小化 model function
minp‾(J(θ‾(k)+p‾))≈minp‾(m(k)(0‾+p‾))\min_{\underline p}\left(J(\underline\theta^{(k)}+\underline p)\right) \approx \min_{\underline p}\left(m^{(k)}(\underline 0 + \underline p)\right) pmin(J(θ(k)+p))≈pmin(m(k)(0+p)) -
信任域(TR)方法还计算当前迭代 的 region of trust TΔ\mathcal T_\DeltaTΔ 。 如果下一个迭代点 θ‾(k+1)=θ‾(k)+p‾\underline\theta ^{(k + 1)} = \underline\theta ^{(k)} + \underline pθ(k+1)=θ(k)+p 还在这个信任域内,则该 model function 将很好地近似于原始目标函数。
-
很可能,这个近似在信任域之外不成立
-
近似模型的quality计算指标:(分子表示函数实际减小的值;分母表示近似模型减少的值)
ρ(k)=J(θ‾(k))−J(θ‾(k)+p‾)m(k)(0‾)−m(k)(p‾)\rho^{(k)} = \frac{J(\underline\theta ^{(k)})-J(\underline\theta ^{(k)}+\underline p)}{m^{(k)}(\underline 0)-m^{(k)}(\underline p)} ρ(k)=m(k)(0)−m(k)(p)J(θ(k))−J(θ(k)+p)- ρ(k)<1\rho ^{(k)} < 1ρ(k)<1 表示模型函数下降速度快于原始函数
- ρ(k)=1\rho ^{(k)} = 1ρ(k)=1 表示完美契合
- ρ(k)>1\rho ^{(k)} > 1ρ(k)>1 表示原始函数的下降速度比模型函数的下降速度快
因此,近似模型函数 m(k)(p‾)m^{(k)}(\underline p)m(k)(p) 进行了优化 w.r.t 迭代增量 p‾\underline pp ,且该解限制其在信赖域范围内
minp‾{m(k)(p‾)}w.r.tp‾∈TΔ\min_{\underline p}\left\{m^{(k)}(\underline p)\right\}\quad w.r.t \quad\underline p\in\mathcal T_{\Delta} pmin{m(k)(p)}w.r.tp∈TΔ
-
信赖域算法同时优化步长和搜索方向,而线搜索算法有一个顺序的方法
Trust region methods optimize the step length and the search direction simultaneously ;Line search algorithms have a sequential approach
数学模型
基本形式
-
信赖域算法:通常选取二次函数(quadratic model function)逼近真实模型的
J(θ‾(k)+p‾)=J(θ‾(k))+[dJ(θ‾)dθ‾∣θ‾(k)]Tp‾+12p‾TB‾(k)p‾⏟m(k)(p‾)J(\underline \theta^{(k)} + \underline p) = \underbrace{J(\underline\theta^{(k)}) +\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right]^T\underline p + \frac12\underline p^T\underline B^{(k)}\underline p }_{m^{(k)}(\underline p)} J(θ(k)+p)=m(k)(p)J(θ(k))+⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤Tp+21pTB(k)p和拟牛顿法法的近似“损失函数”一样
如果B‾(k)\underline B^{(k)}B(k) 选择为Hessian,则为TR的牛顿方法。一般情况下会(比如 Hessian非正定的时候)用对称非奇异矩阵 B‾(k)\underline B^{(k)}B(k) 去近似Hessian矩阵;
-
在每次迭代中半径为Δ(k)\Delta^{(k)}Δ(k) 的球用来定义信赖域的范围 TΔ\mathcal T_\DeltaTΔ
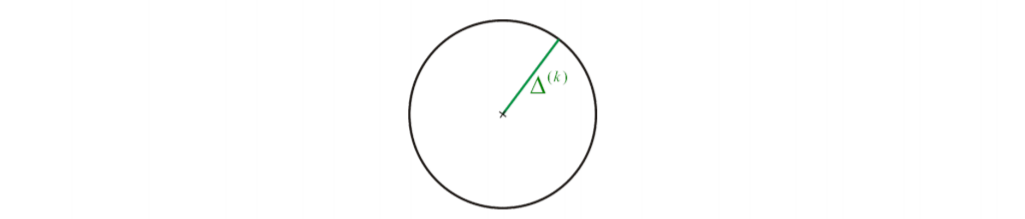
-
因此,我们必须解决下面的优化子问题:关于 $p $ 的带约束的最优化问题,
minp‾{m(k)(p‾)}=minp‾{J(θ‾(k))+[dJ(θ‾)dθ‾∣θ‾(k)]Tp‾+12p‾TB‾(k)p‾}\min_{\underline p}\left\{m^{(k)}(\underline p)\right\} =\min_{\underline p} \left\{ J(\underline\theta^{(k)}) +\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right]^T\underline p + \frac12\underline p^T\underline B^{(k)}\underline p \right\} pmin{m(k)(p)}=pmin⎩⎪⎨⎪⎧J(θ(k))+⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤Tp+21pTB(k)p⎭⎪⎬⎪⎫
要求:参数 ppp 被限制在一个球形区域内
∣∣p‾∣∣2≤Δ(k)\left|\left| \underline p\right| \right|_2 \le \Delta^{(k)} ∣∣∣∣p∣∣∣∣2≤Δ(k)
Δ(k)\Delta^{(k)}Δ(k) 的选择
近似模型的quality计算指标:
ρ(k)=J(θ‾(k))−J(θ‾(k)+p‾)m(k)(0‾)−m(k)(p‾)\rho^{(k)} = \frac{J(\underline\theta ^{(k)})-J(\underline\theta ^{(k)}+\underline p)}{m^{(k)}(\underline 0)-m^{(k)}(\underline p)} ρ(k)=m(k)(0)−m(k)(p)J(θ(k))−J(θ(k)+p)
其中分子表示函数实际减小的值;分母表示近似模型减少的值。
- 如果 ρ(k)<0\rho ^{(k)} < 0ρ(k)<0,一般情况下分母不可能小于0,因为目标函数求解的是最小值;此时说明分子小于0,即下一个目标点比上一步大,此时需要舍弃。
- 如果 0<ρ(k)≈00<\rho ^{(k)} \approx 00<ρ(k)≈0 大于0,但是接近0,说明模型(分母)变化范围比较大,但是实际(分子)改变比较小,此时应该减少信赖域范围Δk
- 0<ρ(k)<10< \rho ^{(k)} < 10<ρ(k)<1 大于0但是明显小于1,表示模型函数下降速度快于原始函数,此时可以不用调整
- 0<ρ(k)≈10< \rho ^{(k)} \approx 10<ρ(k)≈1 大于0并且接近1,表明近似效果好,可以适当增加信赖域半径Δk
- ρ(k)>1\rho ^{(k)} > 1ρ(k)>1 表示原始函数的下降速度比模型函数的下降速度快
信赖域的大小对于每步的效果直观重要. 若信赖域过小, 则算法可能就会错过充分下降的机会; 若过大, 信赖域中模型m**k的极小点可能就与目标函数f的极小点相距甚远, 从而又得增大信赖域.
而信赖域算法是根据一定的原则,直接确定位移 sk ,同时,与一维搜索不同的是,它并没有先确定搜索方向 dk 。如果根据“某种原则”确定的位移能使目标函数值充分下降,则扩大信赖域;若不能使目标函数值充分下降,则缩小信赖域。如此迭代下去,直到收敛
信赖域算法流程
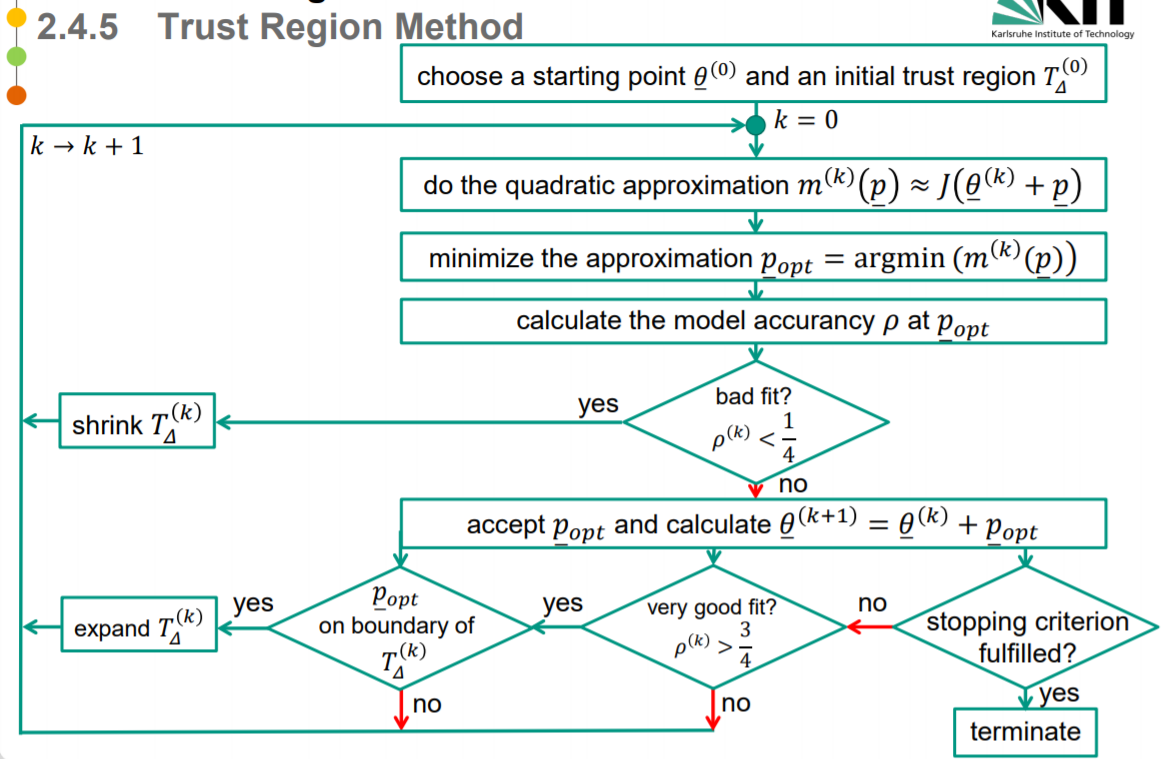
由此我们得到信赖域算法的步骤
-
给出初始点 θ‾(0)\underline\theta^{(0)}θ(0) 和初始信赖域半径 Δ(0)\Delta^{(0)}Δ(0),开始迭代 k
-
计算模型在第k步的近似 m(k)m^{{(k)}}m(k):求解最优化子问题,得到试探步长 p‾\underline pp。
-
求解 model accurancy ρ\rhoρ at p‾\underline pp
-
若 ρ(k)≤14\rho^{(k)}≤\frac14ρ(k)≤41,缩小(shrink)信赖域半径,令
Δ(k+1)=14Δ(k)\Delta^{(k+1)} = \frac14 \Delta^{(k)} Δ(k+1)=41Δ(k)
k = k + 1 返回第一步 -
else:
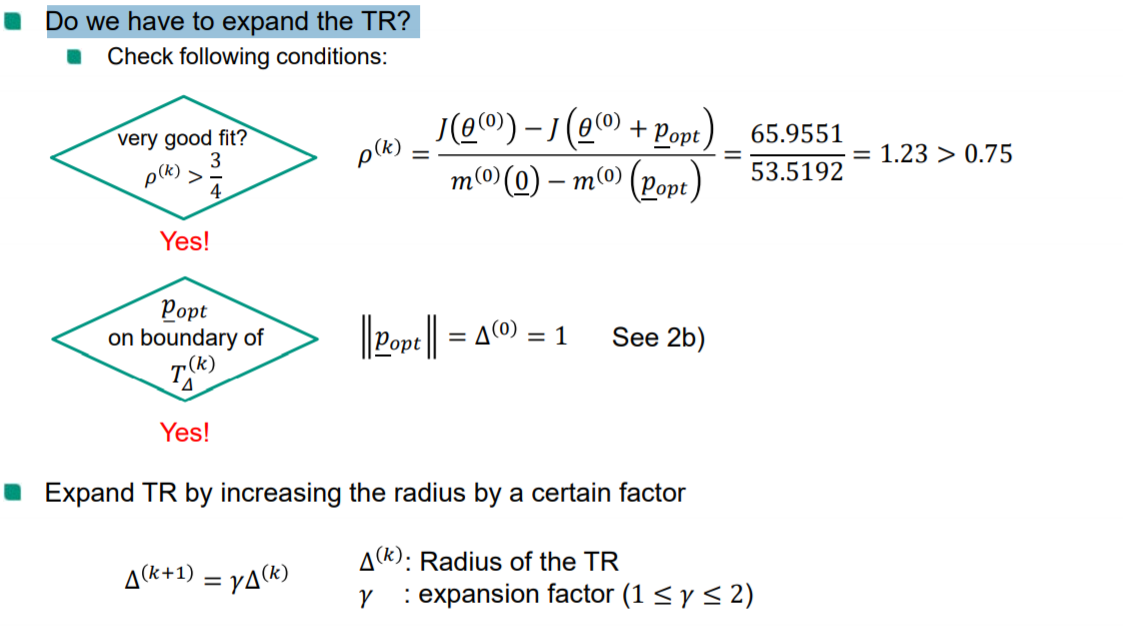
- 若 ρ(k)>0.75\rho^{(k)}>0.75ρ(k)>0.75,扩大信赖域半径,使得 Δk+1=2Δ\Delta_{k+1}=2\DeltaΔk+1=2Δ。
- 若0.25<rk≤0.750.25<r_k\le 0.750.25<r**k≤0.75。维持当前信赖域半径。
- 若rk<0r_k<0r**k<0,缩小信赖域重新计算当前试探步长。
[关于子问题的最优解]
https://blog.csdn.net/fangqingan_java/article/details/46956643
信赖域问题的子问题表示为:
minp‾{m(k)(p‾)}=minp‾{J(θ‾(k))+[dJ(θ‾)dθ‾∣θ‾(k)]Tp‾+12p‾TB‾(k)p‾}\min_{\underline p}\left\{m^{(k)}(\underline p)\right\} =\min_{\underline p} \left\{ J(\underline\theta^{(k)}) +\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right]^T\underline p + \frac12\underline p^T\underline B^{(k)}\underline p \right\} pmin{m(k)(p)}=pmin⎩⎪⎨⎪⎧J(θ(k))+⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤Tp+21pTB(k)p⎭⎪⎬⎪⎫
该问题为标准的带不等式约束的二次优化问题,可以根据KKT条件(后面会深入介绍)得到该问题的最优解
定理 1
向量 p‾∗\underline p^*p∗ 为信赖域子问题的最优解,仅当 p‾∗\underline p^*p∗ 是可行解,且存在标量 λ≥0\lambda \ge 0λ≥0 使得下面的三个条件成立:

其中第二个条件又称为互补条件. 此定理揭示了信赖域方法的优势: 就算B**k是不定的, 我们仍然有子问题达到全局极小的充要条件. 相比之下, 其他方法往往至多有充分条件.
从下图中可以看出最优解 p‾∗\underline p^*p∗ 和参数λ\lambdaλ 的关系
-
当半径参数 Δ=Δ1\Delta = \Delta _1Δ=Δ1 时,最优解为 p3p^3p3 此时相当于没有约束,此时 λ=0\lambda= 0λ=0
-
当半径参数 Δ=Δ2\Delta = \Delta _2Δ=Δ2 时,最优解被球形约束限制,此时满足 Δ=∣∣p∗∣∣Δ=||p^∗||Δ=∣∣p∗∣∣,根据上面条件(a)有
λp∗=−Bp∗−g\lambda p^* = -Bp^*-g λp∗=−Bp∗−g
如果能够找到这样的p满足这些条件就能找到最优解。
⭕折线算法 Dog-Leg Method
目的:找到最小化问题的近似解
折线算法可用于B‾(k)\underline B^{(k)}B(k)为正定的情形
定义完全步(Full Step)
我们在线搜索牛顿法时有:

对于TR子优化问题
minp‾{m(k)(p‾)}=minp‾{J(θ‾(k))+[dJ(θ‾)dθ‾∣θ‾(k)]Tp‾+12p‾TB‾(k)p‾}\min_{\underline p}\left\{m^{(k)}(\underline p)\right\} =\min_{\underline p} \left\{ J(\underline\theta^{(k)}) +\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right]^T\underline p + \frac12\underline p^T\underline B^{(k)}\underline p \right\} pmin{m(k)(p)}=pmin⎩⎪⎨⎪⎧J(θ(k))+⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤Tp+21pTB(k)p⎭⎪⎬⎪⎫
求TR中的位移 p‾\underline pp
折线算法
折线算法可用于 B‾(k)\underline B^{(k)}B(k) 为正定的情形。寻找信赖域半径 Δ(k)\Delta^{(k)}Δ(k) 和最优解 p‾∗(k)(Δ)\underline p^{*(k)}(\Delta)p∗(k)(Δ) 之间的关系。
以下省去上标k, 并以 p‾(Δ)\underline p (\Delta)p(Δ) 表示解以强调其对 $\Delta $ 的依赖性.
-
使用高斯牛顿法得到迭代步长:当 p‾(k)≤Δ(k)\underline p^{(k)}\le \Delta^{(k)}p(k)≤Δ(k)时 (信赖域非常大), 显然应当有 p‾∗(k)(Δ)\underline p^{*(k)}(\Delta)p∗(k)(Δ)
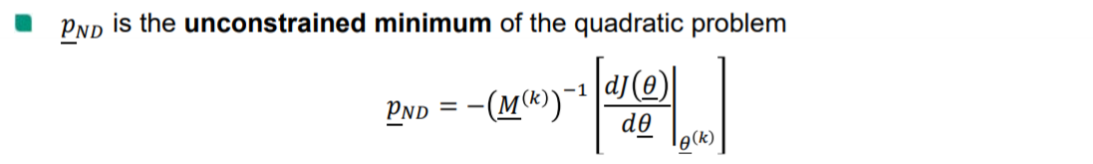
若计算出p‾ND<Δ\underline p_{ND}<\DeltapND<Δ 已经不用继续计算下去 – case 1
-
【p‾t\underline p_{t}pt】当 p‾(k)>>Δ(k)\underline p^{(k)} >> \Delta^{(k)}p(k)>>Δ(k) 时(信赖域非常小), 可认为 m(k)(p‾)m^{(k)}(\underline p)m(k)(p) 问题中的中的二次项(梯度)对子问题的求解影响较小, 从而忽略二次项,即:
m(k)(p‾)=J(θ‾(k))+[dJ(θ‾)dθ‾∣θ‾(k)]T⏟gTp‾tm^{(k)}(\underline p) =J(\underline\theta^{(k)}) +\underbrace{\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}}\right]^T}_{g^T}\underline p_{t} m(k)(p)=J(θ(k))+gT⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤Tpt
calculate the exact minimum of quadratic function along the stepest descent function is equal to 求二次函数的精确最小值沿最小步下降函数等于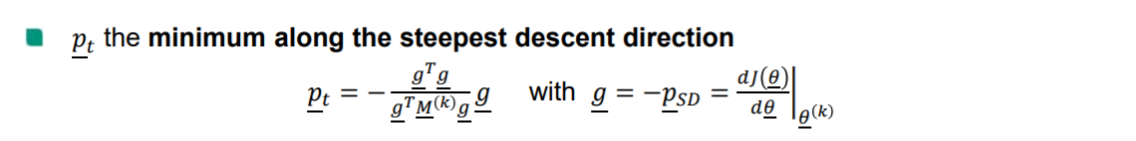
-
ps【p‾s\underline p_sps】
p‾s=p‾ND−p‾t=−[B‾(k)]−1[dJ(θ‾)dθ‾∣θ‾(k)]+[dJ(θ‾)dθ‾∣θ‾(k)]=[I−[B‾(k)]−1][dJ(θ‾)dθ‾∣θ‾(k)]\underline p_s =\underline p_{ND} -\underline p_t =- [\underline B^{(k)}]^{-1} \left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right] + \left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right]=\left[I-[\underline B^{(k)}]^{-1}\right]\left[\frac{dJ(\underline\theta)}{d\underline\theta}\Bigg|_{\underline\theta^{(k)}} \right] ps=pND−pt=−[B(k)]−1⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤+⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤=[I−[B(k)]−1]⎣⎡dθdJ(θ)∣∣∣∣∣θ(k)⎦⎤
我们用 p‾(τ);τ∈[0,2]\underline p(\tau);\tau\in[0,2]p(τ);τ∈[0,2] 表示折线轨迹, 其严格的数学表达为
KaTeX parse error: No such environment: equation at position 30: …\tau) = \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \left\{ \begin…
根据折线算法得到的就是折线轨迹与信赖域边界的交点
对半径为 Δ\DeltaΔ 的信赖域使用DogLeg方法计算出来的步长为
KaTeX parse error: No such environment: equation at position 30: …\tau) = \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \left\{ \begin…
可以看到,DogLeg方法实际上使用了如下策略:
-
如果高斯牛顿法的步长小于信赖域半径,则等同于高斯牛顿法
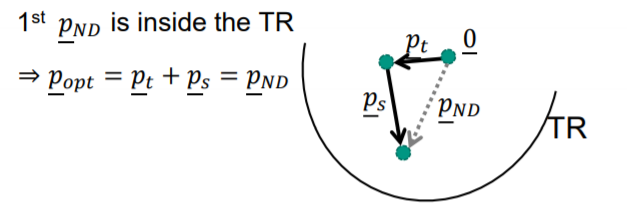
-
如果高斯牛顿法和梯度下降法步长都大于信赖域半径,则将梯度下降法的步长缩放到信赖域半径。

求$\tau $ 归一法
-
如果不满足以上条件,则以连接二条轨迹,与信赖域边界相交于某一点d,从原点指向d的向量即为本次迭代的步长。


Direct Search Methods 直接搜索法
- Box Search
- Section 坐标搜索算法
- Nelder Mead 单纯形
有时候目标函数的梯度不可用
介绍
- 首先,直接搜索方法在实践中效果很好
- 不需要梯度信息
- 一些方法只使用目标函数JJJ在特定搜索点的排名信息, 比当 JJJ 不存在数值分析性
缺点:
- 有时直接搜索方法不收敛,不幸的是,收敛性很难证明。
- 在许多情况下,它们在收敛速度方面表现不佳
类型介绍:
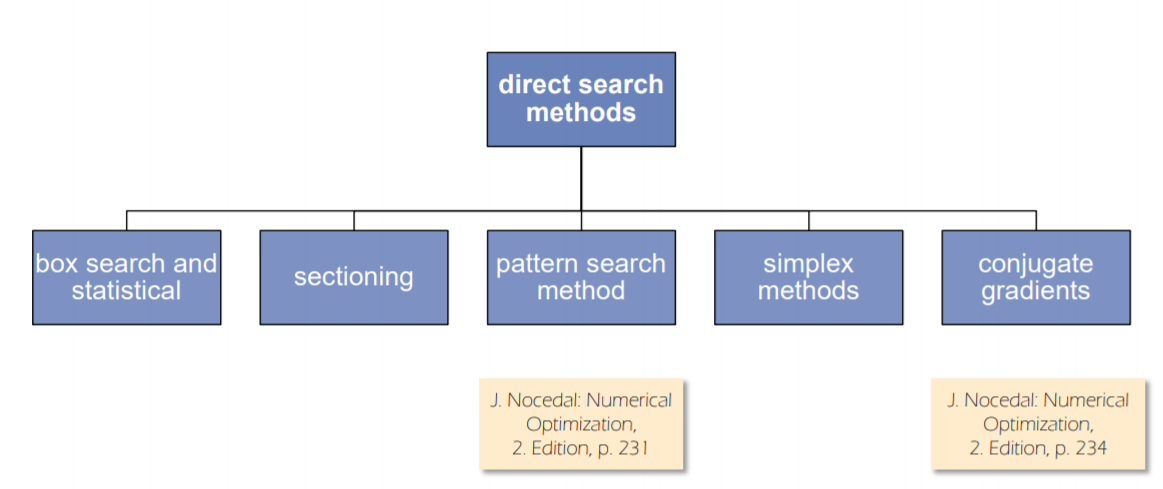
https://blog.csdn.net/m0_37854871/article/details/84969300
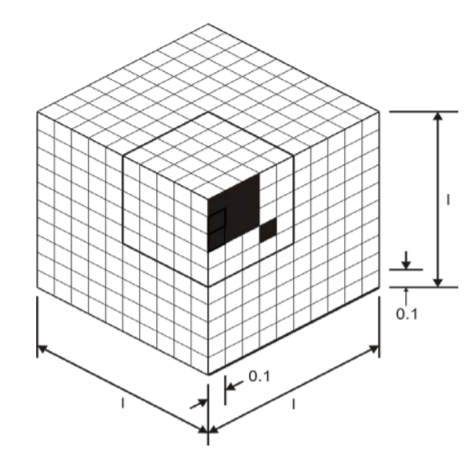
1. Box Search
- 将搜索空间分割成等距的box
- 计算box边缘的所有目标函数值并取最小值
- 缺点:存在维度灾难
- 因此,有一些方法可以使用生物原理(遗传算法)来生成一个boxes子集。
2. Section 坐标搜索算法 (属于线搜索算法)
坐标搜索和模式搜索方法并不从函数值中显式地构建目标函数的模型, 而是从当前迭代点出发沿着特定的方向寻找具有更小函数值的点. 若找到了这样的点, 它们就步进并重复之前的过程, 当然此前可能会对之前的搜索方向做一些改动. 当没有满意的点存在时, 算法就可能会调整沿着当前搜索方向前进的步长, 或直接产生新的搜索方向.
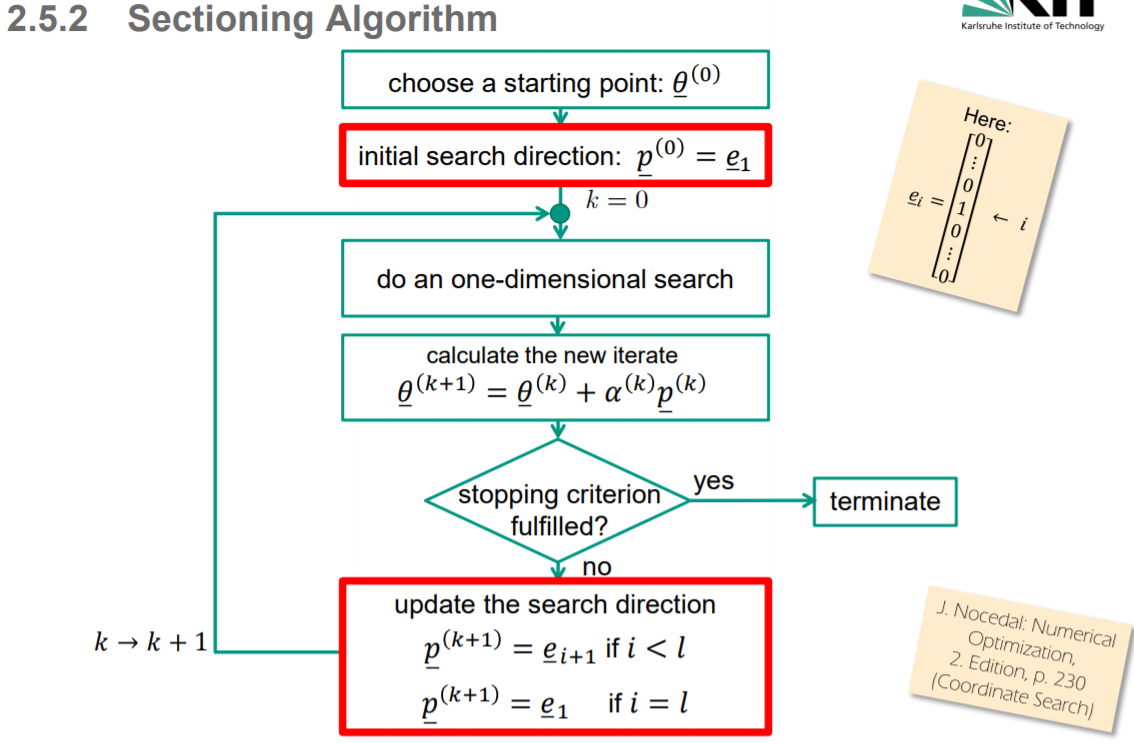
The process of finding a solution might be inefficient or will be even impossible if there are valleys or ridges
坐标搜索方法(也称为坐标下降法或交替变量法) 循环遍历 n 个坐标方向 e1,e2,…,ene_1,e_2,\ldots,e_ne1,e2,…,en, 在每个方向上均以线搜索获取新的迭代点.
一定是先从 θ‾1\underline\theta_1θ1 方向开始的
具体说来, 第一次迭代中, 我们仅改变xxx的第一个分量x1x_1x1并寻找极小(或至少减小)目标函数的这一分量的新值. 下一步迭代中, 则对第二个分量 x2x_2x2进行同样的操作. 在nnn步迭代后, 我们又回到第一个变量重复遍历.
尽管简单直观, 但此法在实际操作中却可能十分低效, 就比如下图中表示的, 我们将坐标搜索方法应用于带两个变量的二次函数上.图中显示, 经几步迭代后, x1,x2x_1,x_2x1,x2向解的行进都明显变慢.
就算坐标搜索收敛于一解, 一般来说它也要比最速下降法慢得多, 并且这一差距随着变量数的增加而越变越大. 不过由于坐标搜索不需要计算梯度∇fk\nabla f_k∇f**k, 且它在变量耦合程度不高时的效果还不错, 因此它仍是优化目标函数的有效方法.
a sectioning algorithm would never reach the real minimum at [ ] * 0 0 T θ = exactly. (Or it would need an infinite number of iterations).
https://blog.csdn.net/m0_37854871/article/details/84969300#3__114
3. ⭕Nelder Mead
-
目的:使用更复杂的方法确定搜索方向
-
记住:没有可用的梯度信息
-
想法:评估几个点,对它们进行排名,试图通过把最坏的点向最好的点移动来改善结果
Idea: Evaluate several points, rank them, try to improve the result by shifting the worst point in the direction of the best point(s)
定义:Simplex 单纯形
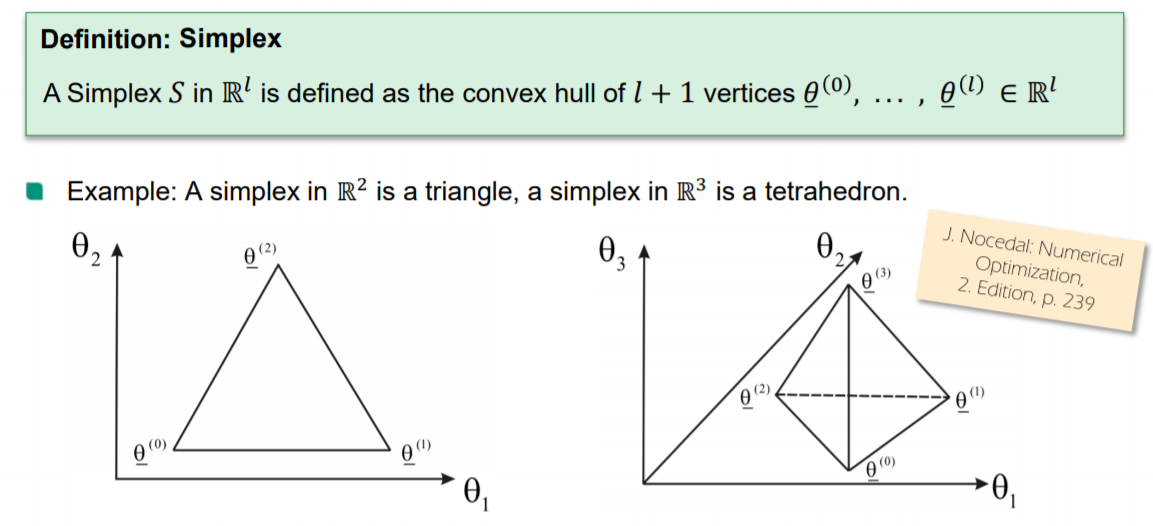
3 个越是 4个顶点
Nelder-Mead单纯形反射方法自其1965年被发明以来一直是广受欢迎的DFO算法。其名称来源于在算法的任意阶段, 我们都保持对单纯形 SSS 的空间 Rl\R^lRl 中的 l+1l+1l+1 个顶点(vertices)追索,它们形成的凸腔构成单纯形. (这一方法与线性规划中的单纯形法没有任何关联)。 给定有顶点 的单纯 θ‾(0),...,θ‾(l)\underline\theta^{(0)},...,\underline\theta^{(l)}θ(0),...,θ(l) 的单纯形SSS , 我们可定义关联矩阵
算法
Nelder-Mead算法中的单次迭代中, 我们移除具有最差函数值的顶点并代之以具更好值的点. 而新点则是通过沿着连接最差顶点与剩余顶点中心的线反射、扩张或收缩单纯形得到。若以这种方式我们无法找到更好的点, 我们就仅保持具最好函数值的点不动,,而令其他的顶点向该值移动以收缩单纯形.
下面我们来详细描述算法的一次迭代过程.
-
该方法生成初始工作单纯形。
-
先定义一些符号: 当前单纯形的 l+1l+1l+1 个顶点 θ‾(0),...,θ‾(l)∈Rl\underline\theta_{(0)},...,\underline\theta_{(l)}\in\R^lθ(0),...,θ(l)∈Rl,计算每个点的目标函数值,并对他们进行排序,满足目标函数值从小到大:
J(θ‾(1))≤J(θ‾(2))≤⋯≤J(θ‾(l+1))J(\underline\theta_{(1)})\le J(\underline\theta_{(2)})\le\cdots \le J(\underline\theta_{(l+1)}) J(θ(1))≤J(θ(2))≤⋯≤J(θ(l+1))
另外对这些点进行命名:- “best vertex”θ‾(1)=θ‾(b)\underline \theta{(1)} = \underline\theta^{(b)}θ(1)=θ(b)
- “second best vertex”θ‾(2)=θ‾(sb)\underline\theta_{(2)} = \underline\theta^{(sb)}θ(2)=θ(sb)
- “second worst vertex”θ‾(l)=θ‾(sw)\underline\theta_{(l)} = \underline\theta^{(sw)}θ(l)=θ(sw)
- “worst vertex”θ‾(l+1)=θ‾(w)\underline\theta_{(l+1)} = \underline\theta^{(w)}θ(l+1)=θ(w)
Remark
in R2\R^2R2 we denote θ‾(sb)=θ‾(sw)=θ‾(m)\underline\theta^{(sb)} = \underline\theta^{(sw)} = \underline\theta^{(m)}θ(sb)=θ(sw)=θ(m) as “middle vertex”
-
通过执行一系列由基本转换组成的转换(transformation),尝试沿着顶点的方向移动(shift)最坏的顶点
- Reflection 反射
- Expansion 扩张
- (inner/outer) Contraction
- Shrinking
1. reflection
每个转换的performance取决于目标函数的局部属性/形状。例如在如下区域进行reflection反射
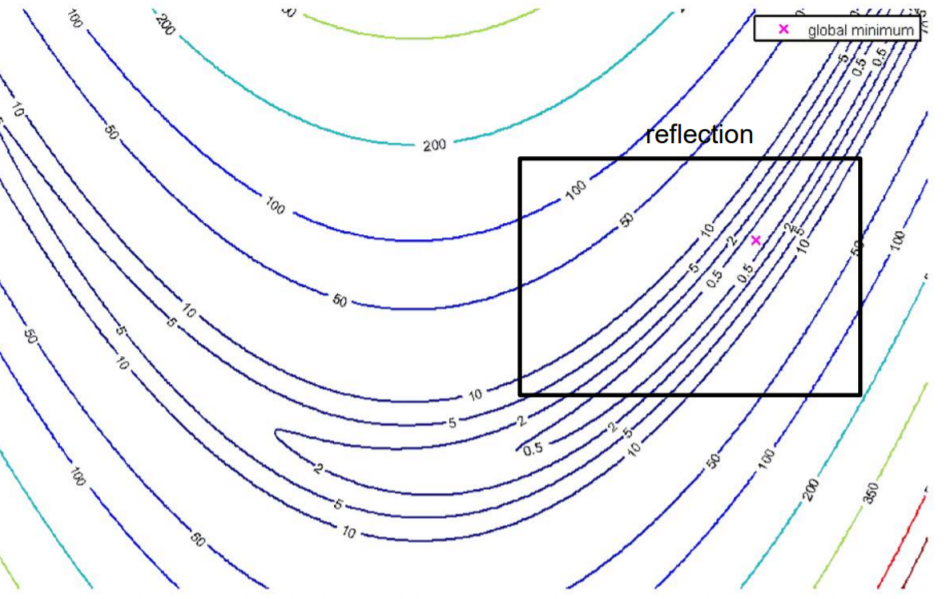
-
将 the worst vertex θ‾(w)\underline\theta ^{(w)}θ(w) 绕 centroid c‾\underline cc reflect 转换:
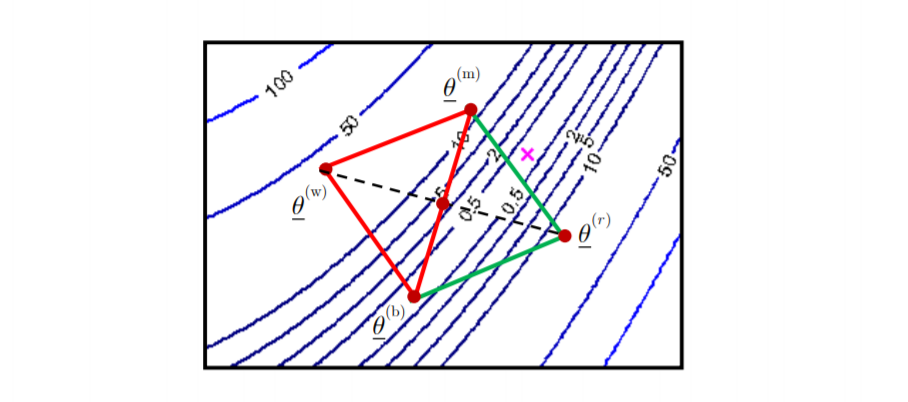
-
计算新点的坐标:
θ‾(r)=c‾+α(c‾−θ‾(w))α∈R\underline\theta^{(r)} = \underline c + \alpha\left(\underline c - \underline\theta^{(w)}\right)\quad \alpha\in \R θ(r)=c+α(c−θ(w))α∈R
记个点的目标函数值为:
J(θ‾(r))=J(r)J(\underline\theta^{(r)}) = J^{(r)} J(θ(r))=J(r)中心点 c‾\underline cc 怎么计算的?
ccc is the centroid of all vertices other than the worst, the centroid of n arbitrary points is given by
c‾=1n∑i=1nθ‾(i)\underline c = \frac1n\sum_{i=1}^ n\underline\theta_{(i)} c=n1i=1∑nθ(i)
-
反射变换的结果:如果新的点的函数值小于倒数第二差的点,则将最差的点舍弃,将此新点加入

2. Explansion
例如在如下区域进行 explansion
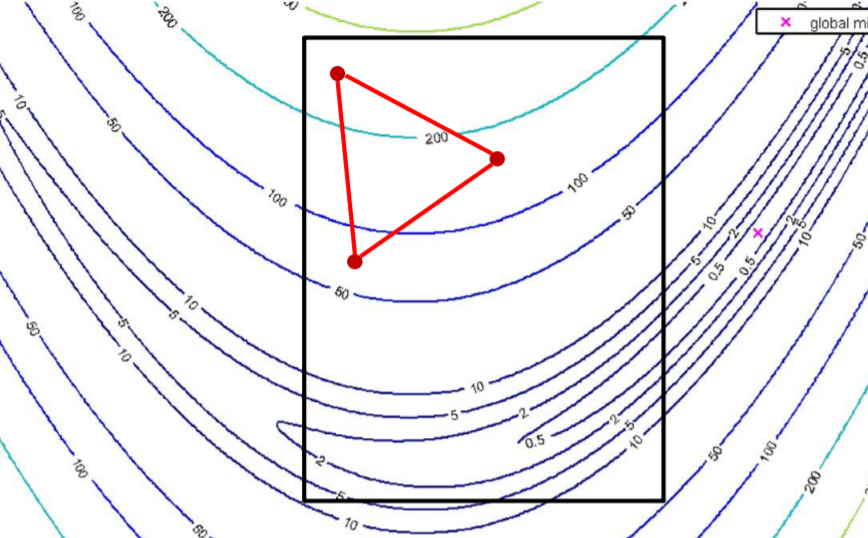
-
假设经过 reflection 得到的新点 θ‾(r)\underline\theta^{(r)}θ(r) 的目标函数值比最优点还低:J(r)<J(b)J^{(r)}<J^{(b)}J(r)<J(b),尝试进一步改进解决方案并扩展单纯形
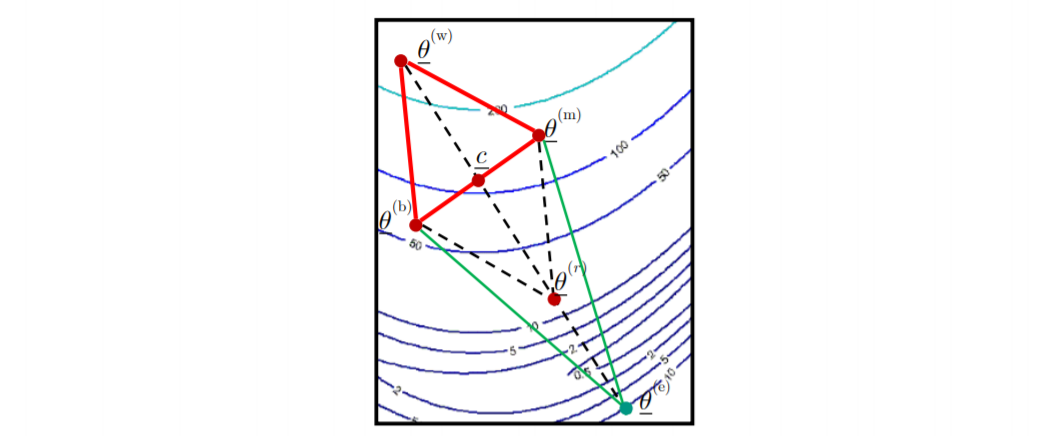
-
计算扩展的新点θ‾(e)\underline\theta^{(e)}θ(e)的新坐标
θ‾(e)=c‾+γ(c‾−θ‾(w))γ∈R\underline\theta^{(e)} = \underline c + \gamma(\underline c - \underline\theta^{(w)}) \quad \gamma \in\R θ(e)=c+γ(c−θ(w))γ∈R -
扩张变换的结果:如果新的点的函数值小于被扩张的点,将此新点加入替换被扩张的点

3. outer contraction
例如在如下区域进行 outer contraction
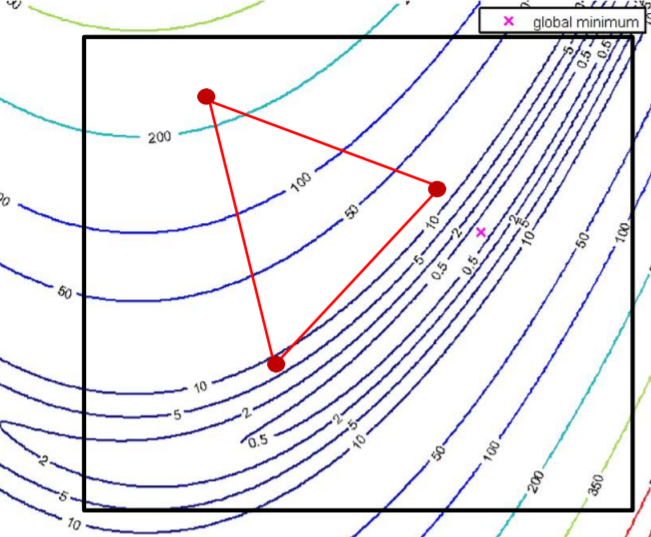
尝试对 reflect 后的点进行 outer contraction
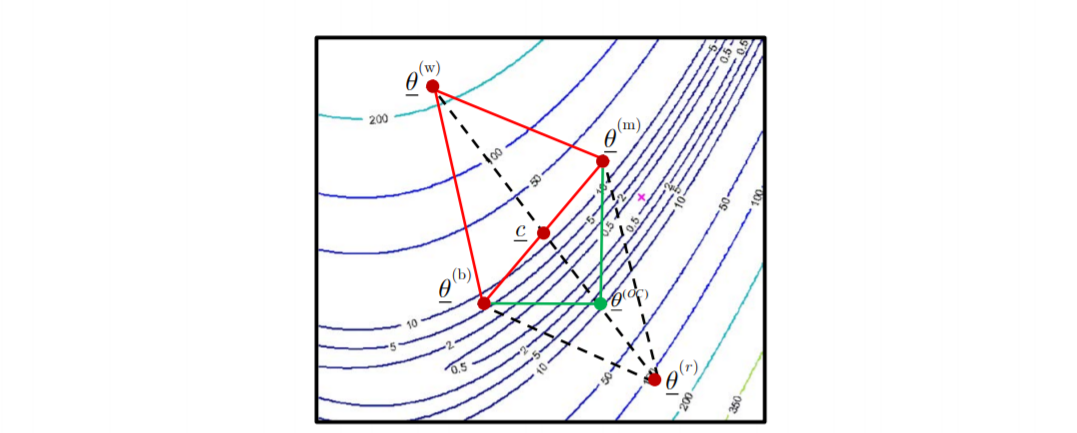
-
由 θ‾(r)\underline\theta^{(r)}θ(r) outer contraction 到点 θ‾(oc)\underline\theta^{(oc)}θ(oc)
θ‾(oc)=c‾+β(θ‾(r)−c‾)β∈R\underline\theta^{(oc)} = \underline c + \beta(\underline\theta^{(r)} - \underline c) \quad \beta \in \R θ(oc)=c+β(θ(r)−c)β∈R -
outer contraction 变换的结果:如果新的点的函数值小于 θ‾(r)\underline\theta^{(r)}θ(r) 的目标函数值,将此新点加入替换原来的点

4. inner contraction
例如在如下区域进行 inner contraction
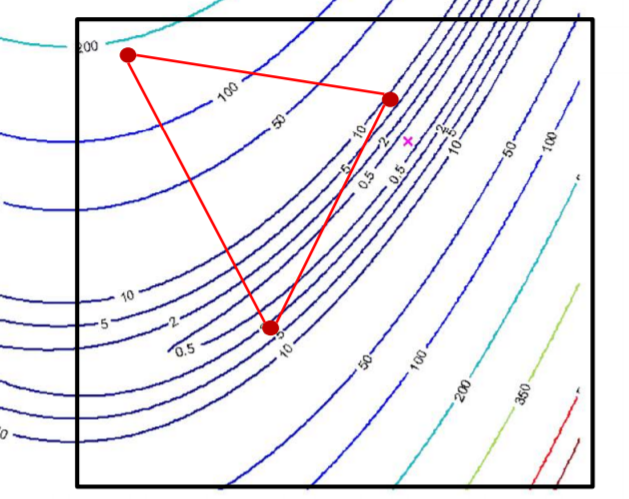
尝试对 the original simplex 进行 inner contraction,即不将 最差的点先进行 反射操作,再 contraction,而直接对最差的点进行 contraction
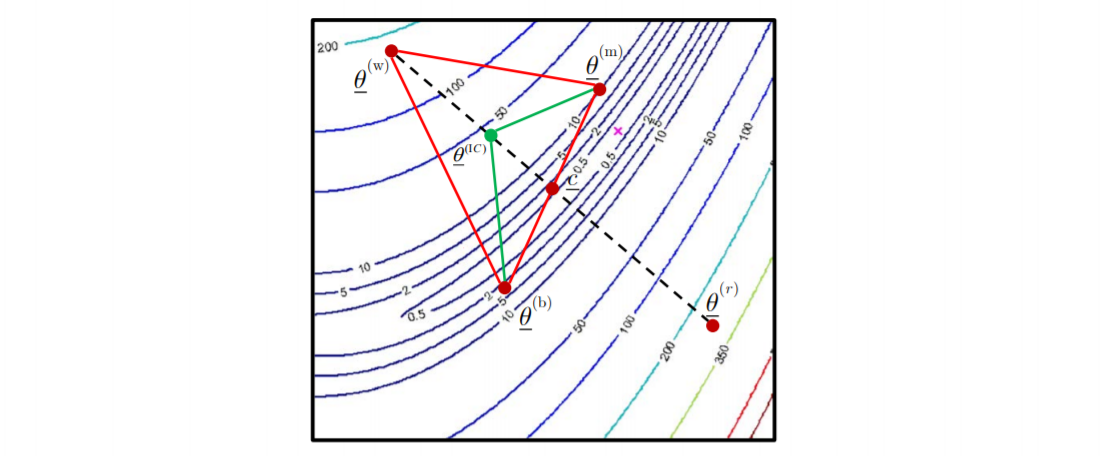
-
由 θ‾(w)\underline\theta^{(w)}θ(w) outer contraction 到点 θ‾(ic)\underline\theta^{(ic)}θ(ic)
θ‾(ic)=c‾+β(θ‾(w)−c‾)β∈R\underline\theta^{(ic)} = \underline c + \beta(\underline\theta^{(w)} - \underline c) \quad \beta \in \R θ(ic)=c+β(θ(w)−c)β∈R -
inner contraction 变换的结果:如果新的点的函数值小于 θ‾(w)\underline\theta^{(w)}θ(w) 的目标函数值,将此新点加入替换原来的点

5. shinking
例如在如下区域进行 shinking
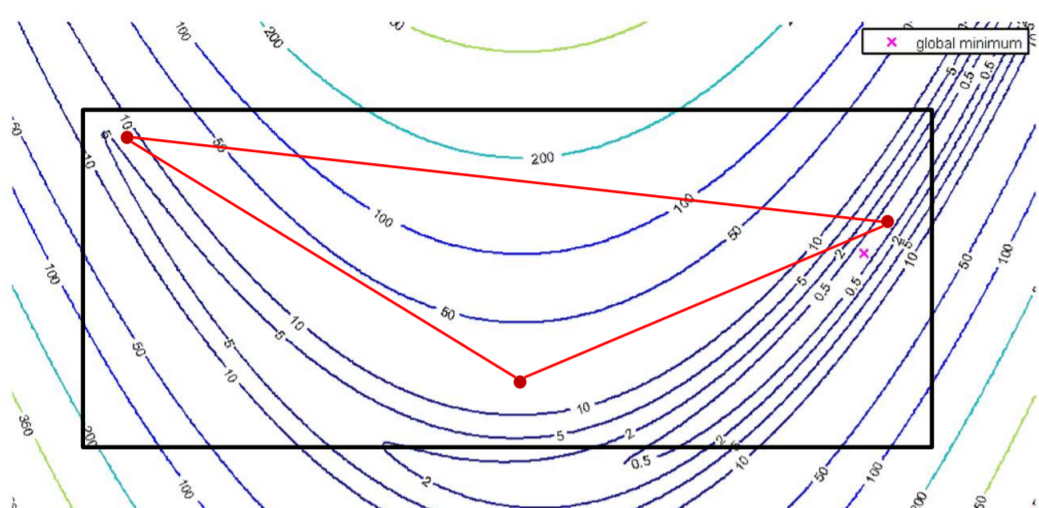
保留最忧点不动,其它点按比例缩放
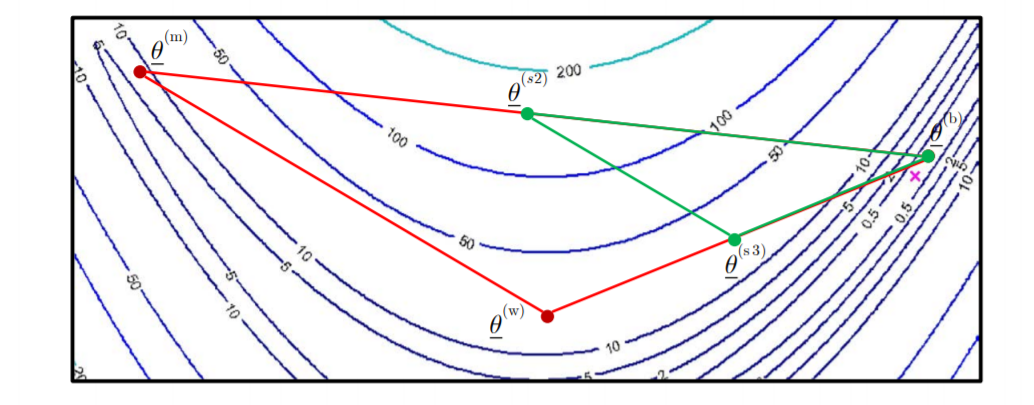
shrinking的结果为:

总结 Nelder Mead 算法流程:
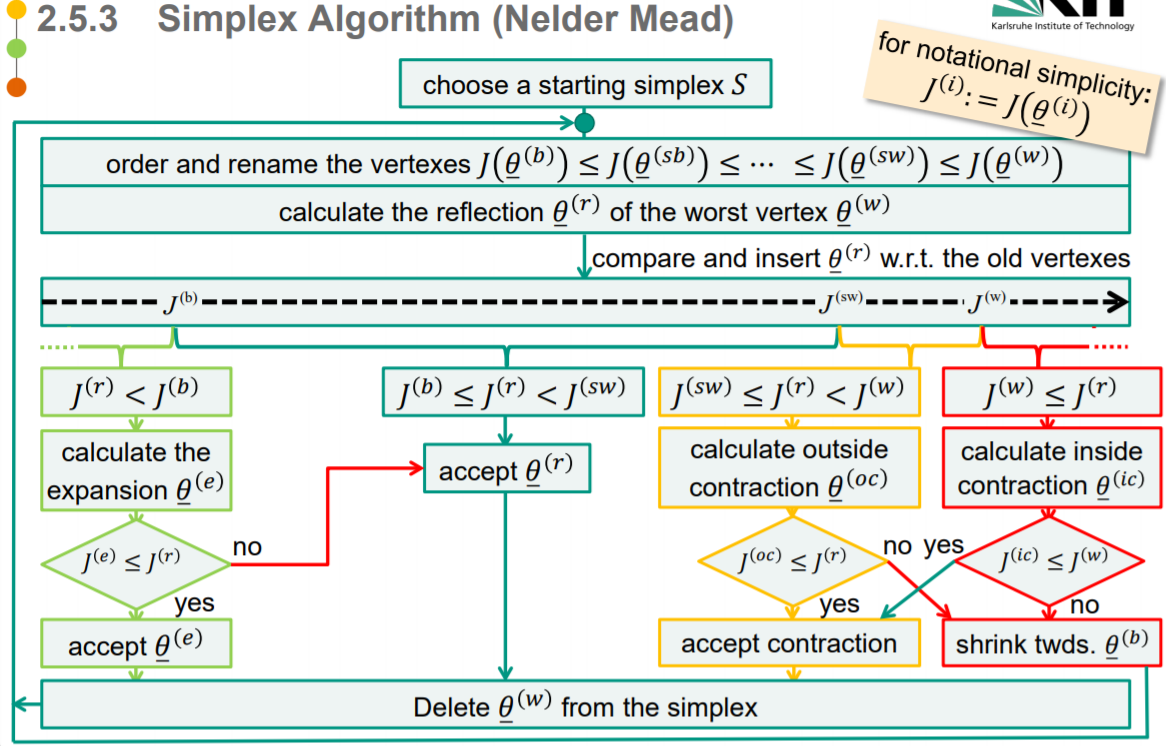
Final remarks:
- 尽管在1998年已经推导出了一组目标函数和初始simplexe且具有可证明的收敛性,但对该算法的严格分析仍是困难的。然而,即使在简单的情况下,算法也可能失败。
- 单纯形算法(Nelder Mead)与数值数学和以前的ODS术语中涉及的线性规划的数值单纯形算法无关。
Nonlinear Least Squares(NLS) 非线性最小二乘法 – LMA
一

二:问题定义
【非线性最小二乘法】
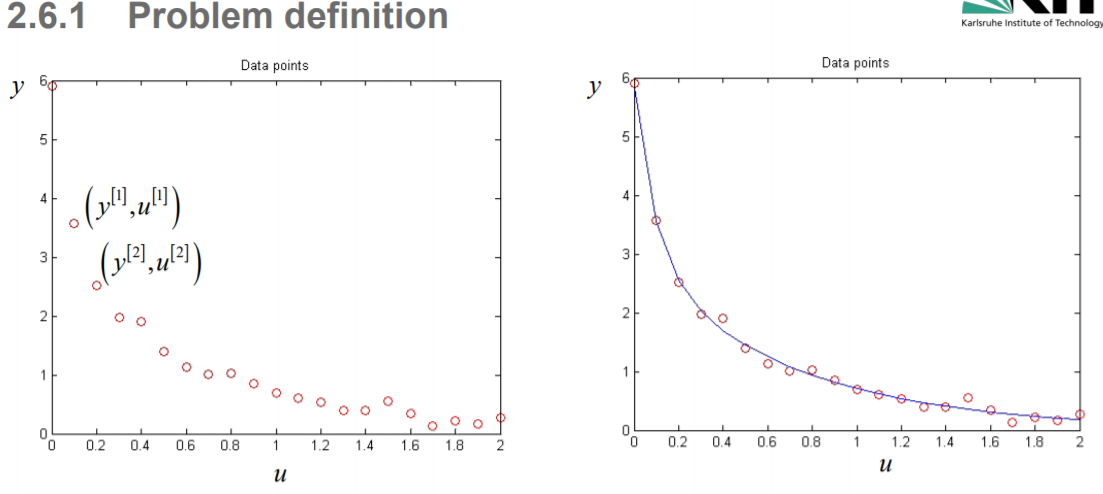
-
目的:找到适合给定输入(𝑢)和最佳输出数据(𝑦)的最佳曲线(二次)参数(parameterization)
-
例子:找到下面曲线的参数 θ1,θ2,θ3,θ4\theta_1,\theta_2,\theta_3,\theta_4θ1,θ2,θ3,θ4,使它能够最优拟合数据
f(u)=θ1e(θ2u)+θ3e(−θ4u)f(u) = \theta_1e^{(\theta_2 u)}+\theta_3e^{(-\theta_4 u)} f(u)=θ1e(θ2u)+θ3e(−θ4u)
-
假设我们有一组给定的(测量的)数据 y‾[1],y‾[2],...,y‾[N]\underline y^{[1]},\underline y^{[2]},...,\underline y^{[N]}y[1],y[2],...,y[N] , 以及对应的输入点 u‾[1],u‾[2],...,u[N]\underline u^{[1]},\underline u^{[2]},..., u^{[N]}u[1],u[2],...,u[N]
-
定义一个模型函数(moderl function),以最优拟合这些测量值
y‾=m‾(u‾,θ‾)\underline y = \underline m(\underline u,\underline \theta) y=m(u,θ) -
定义一个目标函数(objectivefunction):使用测量曲线和参数化曲线的平方和
Using the sum of squares between measurement and parameterized curve
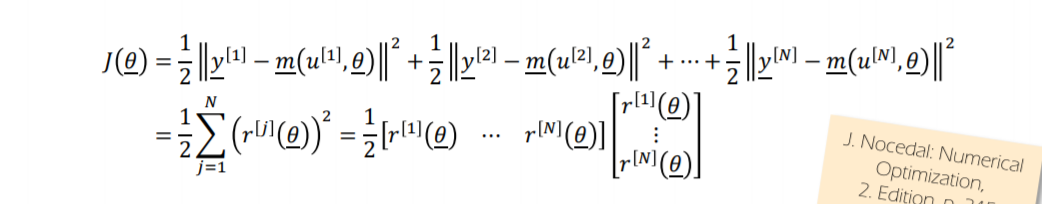
-
使用第2章的搜索技术来最小化目标函数 求解

J(θ‾)=12∣∣3−θ1eθ2∣∣2+12∣∣11−2θ2eθ3∣∣2+12∣∣26−3θ3eθ4∣∣2J(\underline\theta)=\frac12||3-\theta_1e^{\theta_2}||^2+\frac12||11-2\theta_2e^{\theta_3}||^2 + \frac12||26-3\theta_3e^{\theta_4}||^2 J(θ)=21∣∣3−θ1eθ2∣∣2+21∣∣11−2θ2eθ3∣∣2+21∣∣26−3θ3eθ4∣∣2

线性 model function为:
y=ax+by = ax+b y=ax+b
则优化问题为:
mina,bJ=∑i=010(yi−(axi+b))2\min_{a,b} J=\sum_{i=0}^{10} (y_i-(ax_i+b))^2 a,bminJ=i=0∑10(yi−(axi+b))2
三:问题的解
NLS问题的有趣特性是目标函数的 梯度 和 Hessian 矩阵的近似容易求得:
-
Gradient of J(θ)J(\theta)J(θ)
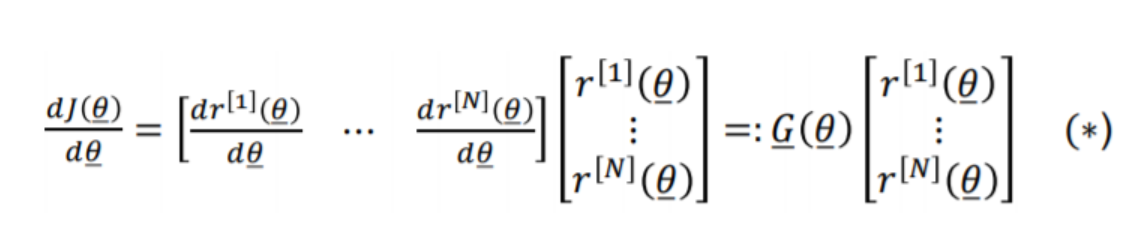
-
The approximation of the Hessian of J(θ‾)J(\underline\theta)J(θ)
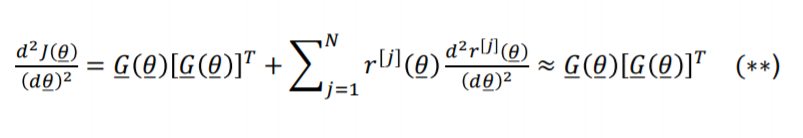
由高斯牛顿法

-
如果我们现在应用牛顿法得到高斯牛顿搜索方向 p‾GN\underline p_{GN}pGN (参见Ch.2幻灯片47)
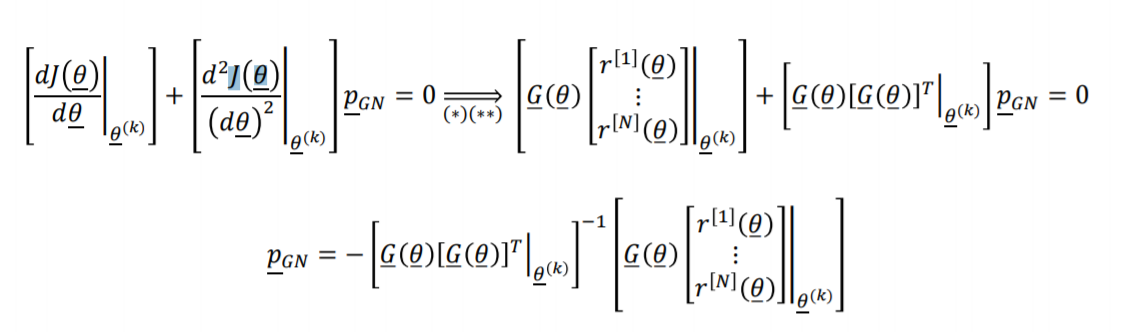
-
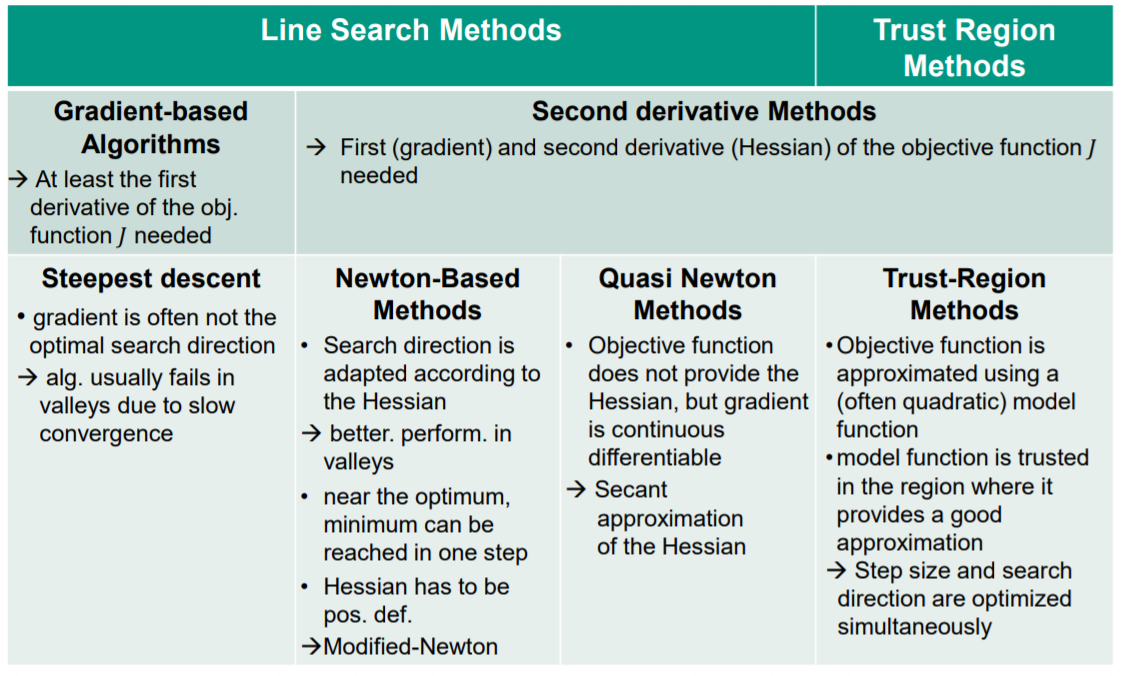
在改进的牛顿法中插入(∗)和(∗∗)会得到Levenberg Marquardt搜索方向
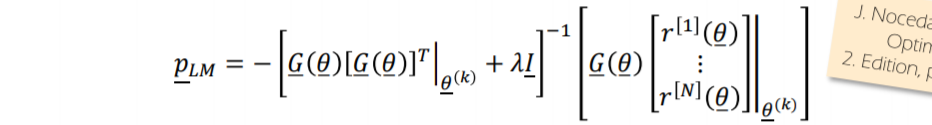
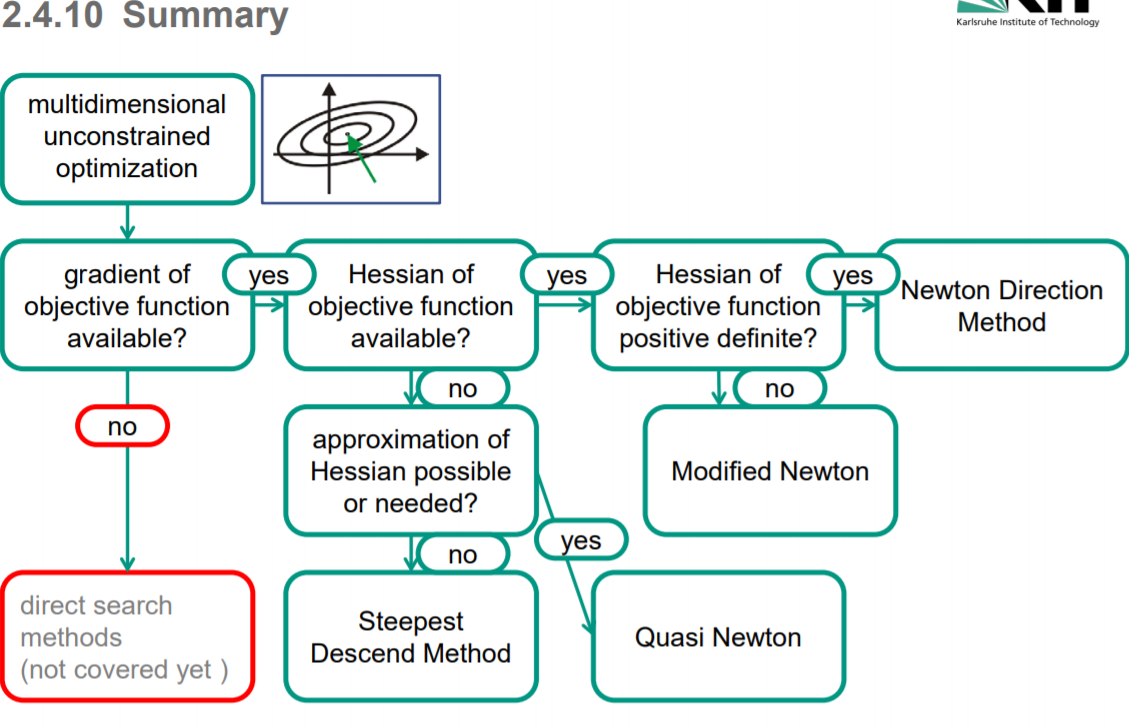
非约束优化总结
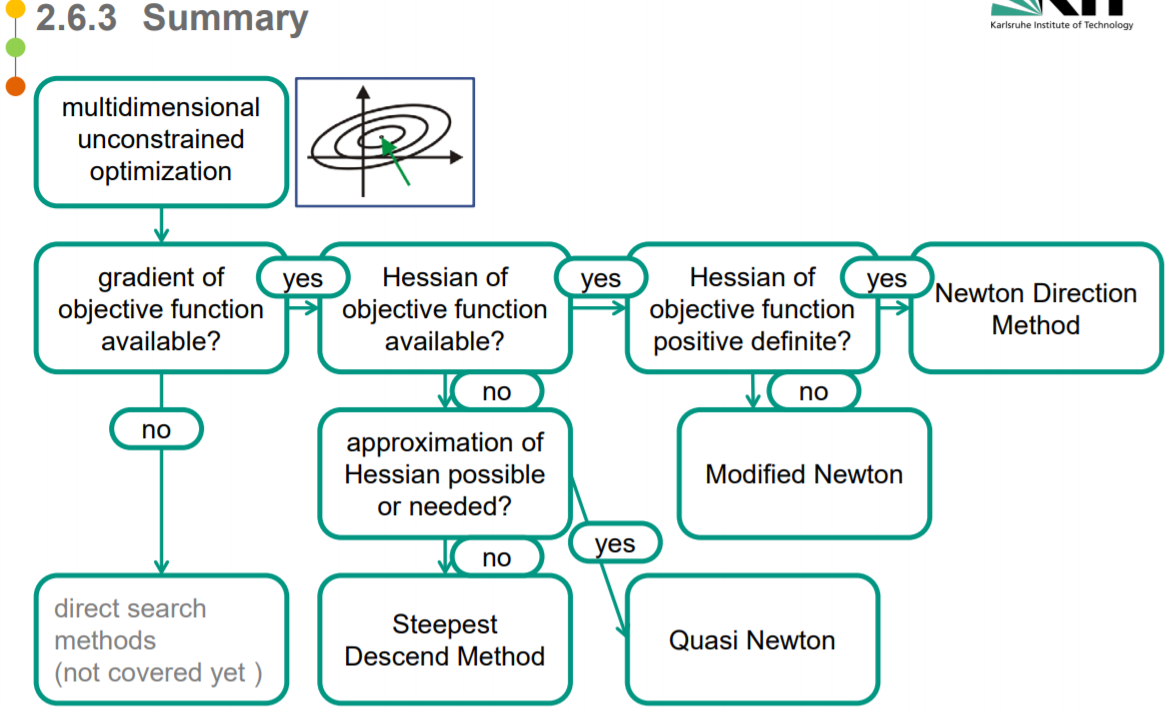
线搜索&信赖域
基于梯度的方法
需要目标函数的一次导数信息
Steepest descent 最速梯度下降法
- 梯度往往不是最优搜索方向
- [代数] 由于收敛速度慢,通常在谷中失败
基于Hessian的方法
需要目标函数的梯度信息和二次 Hessian 信息
牛顿法
- 搜索方向根据Hessian 调整
- better. perform. in valleys
- 在最优值附近,可以一步达到最小值
- Hessian has to be pos. def.
- 如果非正定:Modified-Newton
拟牛顿法
- 目标函数不提供Hessian,但梯度是连续可微的
- Secant approximation of the Hessian
信赖域法
- 目标函数用一个(通常是二次的)模型函数逼近
- 模型函数在信赖域提供了一个很好的近似
- Step size and search direction are optimized simultaneously
直接搜索

无梯度信息
Box Search:维度灾难
Sectioning:
- 沿着坐标轴方向使用线搜索技术确定最小值
- 如果函数包含谷底(例如香蕉函数),则此算法会失效
- 不是所有问题可以由独立优化参数解决
Simplex Algorithm
- 单纯形算法自动适应问题
- 对含有 valleys的问题表现较好
于收敛速度慢,通常在谷中失败
基于Hessian的方法
需要目标函数的梯度信息和二次 Hessian 信息
牛顿法
- 搜索方向根据Hessian 调整
- better. perform. in valleys
- 在最优值附近,可以一步达到最小值
- Hessian has to be pos. def.
- 如果非正定:Modified-Newton
拟牛顿法
- 目标函数不提供Hessian,但梯度是连续可微的
- Secant approximation of the Hessian
信赖域法
- 目标函数用一个(通常是二次的)模型函数逼近
- 模型函数在信赖域提供了一个很好的近似
- Step size and search direction are optimized simultaneously
直接搜索
[外链图片转存中…(img-3UpmtI1z-1603197799950)]
无梯度信息
Box Search:维度灾难
Sectioning:
- 沿着坐标轴方向使用线搜索技术确定最小值
- 如果函数包含谷底(例如香蕉函数),则此算法会失效
- 不是所有问题可以由独立优化参数解决
Simplex Algorithm
- 单纯形算法自动适应问题
- 对含有 valleys的问题表现较好
如若内容造成侵权/违法违规/事实不符,请联系编程学习网邮箱:809451989@qq.com进行投诉反馈,一经查实,立即删除!
相关文章
- Linux异步IO实现方案总结
一、glibc aio 1、名称 由于是glibc提供的aio函数库,所以称为glibc aio。 glibc是GNU发布的libc库,即c运行库。 另外网上还有其他叫法posix aio,都是指glibc提供的这套aio实现方案。 2、主要接口 glibc aio主要包含如下接口:…...
2024/4/22 17:13:00 - Pycharm报错:Function call stack: keras_scratch_graph
代码开头加上 gpus tf.config.experimental.list_physical_devices(GPU) if gpus:try:# Restrict TensorFlow to only use the fourth GPUtf.config.experimental.set_visible_devices(gpus[0], GPU)# Currently, memory growth needs to be the same across GPUsfor gpu in …...
2024/4/23 8:04:39 - 阿斯顿Java
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注…...
2024/4/21 3:17:04 - HHKB Programming Contest 2020 E.Lamps
HHKB Programming Contest 2020 E.Lamps 题目链接 这题我用的排除法,首先可以计算出所有灯的数量 kkk,则总情况数即为 k∗2kk*2^kk∗2k,对每一盏灯,只需要减去使其不亮的情况即可,即算出上下左右的联通的灯的数量 xxx…...
2024/4/16 7:29:40 - gmoj 6823. 【2020.10.17提高组模拟】糖果游戏 「博弈论」
题目 https://gmoj.net/senior/#main/show/6823 题解 这算是我SG函数的入门题吧…… 不妨先考虑每一堆石子中的情况,设fif_ifi表示操作前堆中有 i 个石子时,当前操作的玩家是否是取完这堆石子的那个玩家(记为0/1,0不是1是&am…...
2024/4/6 9:56:26 - Netty原理详解系列(六)---Netty核心组件与基础应用
文章目录1.概述2.Netty核心组件2.1 EventLoop2.2 Channel2.3 ChannelPipeline2.4 ChannelFuture3. 基础应用4. 后续1.概述 通过上一篇博客《Netty原理解析系列(五)—Netty线程模型》中了解了Netty的线程模型,对Netty的整体架构有了一定的认识。这篇文章将介绍Netty…...
2024/4/6 9:56:25 - Java 如何 把base64图片数据转为本地图片
加微心:itmall1024,有学习资源,欢迎来撩!共同成长与进步 项目中用到的把base64图片数据转为本地图片的函数 直接上代码: /*** 替换html中的base64图片数据为实际图片* param html* param fileRoot 本地路径* param se…...
2024/4/6 9:56:24 - 系统与软件命令及网络资源记录
Linux系统 文件夹 打开 shell: CtrlAltTshell 打开 文件夹: nautilus . 查看进程运行路径: ps -ef | grep [proc] ll /proc/[ProcID]/exe软件 IDEA快捷键 快速搜索类: CtrlN 快速搜索文件: CtrlShiftN 快…...
2024/4/20 15:27:32 - 利用umat子程序实现考虑湿热效应的复合材料渐进损伤分析
湿热环境的作用会导致复合材料本身的力学性能变化。 试验研究表明,单向复合材料的力学性能在一定的湿热范围内单调变化,另一方面,湿热环境在复合材料结构内产生湿热变形与应力,导致基体、纤维或界面发生变化或破坏,从而…...
2024/4/6 6:28:49 - Ubuntu下连接raw.githubusercontent.com失败
问题描述: Ubuntu下连接raw.githubusercontent.com失败 wget https://raw.githubusercontent.com/madmashup/targeted-marketing-predictive-engine/master/banking.csv --2020-05-17 17:00:19-- https://raw.githubusercontent.com/madmashup/targeted-marketin…...
2024/4/6 6:28:48 - 设计模式——创建者类型之单例模式
设计模式——创建者类型之单例模式背景说明单例模式代码链接吐槽背景 本人从事开发工作也有多年,目前坐标湖南长沙,以前在各种平台也发过一些文章但是都没有坚持下来; 这个系列是要写设计模式的,将23大设计模式逐一用自己的理解加…...
2024/4/25 8:12:37 - Java-二叉树的前序、中序和后序查询
前序查找的思路分析 1.先判断当前节点是不是自己要找的 2.如果是,则返回当前节点 3.如果不是,则判断当前节点的左子节点是否为空,如果不为空,则递归前序查找 4.如果左递归前序查找,找到节点则返回,若未找到…...
2024/4/19 6:53:07 - 栈溢出之构造函数覆盖返回地址
栈溢出利用已知函数覆盖返回地址 题目:攻防世界 level2 查看文件的保护,发现没有栈哨,可以考虑覆盖返回地址。 利用IDA进行静态分析,找到vulnerable_function()函数 ssize_t vulnerable_function() {char buf; // [esp0h] [eb…...
2024/4/6 6:28:46 - Filecoin筹备三年,上线后就面对内讧、罢工、分叉……搞砸了吗?
加密行业每隔一段时间就有相应的热点,近期最备受关注的项目是 Filecoin。 今天我们不聊去中心化存储的未来,只想看看 Filecoin 的投资回报。主网上线前,很多人对 Filecoin 寄予厚望,但上线后的种种迹象表明:这个几经延…...
2024/4/28 7:44:34 - 计算机网络参考模型
计算机万络参考模型 分层思想 将复杂的流程分解为几个功能相对单一的子过程 优点:整个流程更加清晰,复杂问题简单化; 更容易发现问题,并针对性的解决问题; 开放系统互联参考模型(OSI) OSI模…...
2024/4/6 6:28:43 - Appium的理论和使用
1、Appium的简介和原理 appium是一款开源的,跨平台的UI自动化测试工具,适用于测试原生的或者混合型的移动APP,支持IOS,Android,Firefox OS等平台,同时该框架支持JAVA,Python,PHP等语…...
2024/4/6 9:56:23 - 网络笔记_RSTP快速STP
目录 前言 STP的问题点 问题一:设备从初始状态到完全收敛至少需要30s 问题二:直连端口故障,将另外端口转换为RP端口,需要至少30s 问题三:非直连端口故障 问题四:终端连接上来,需要至少30s 问题五…...
2024/4/6 9:56:22 - MyBatis Generator配置(每个方法都有详细介绍)
快速搭建 1.CommentGenerator package com.longs; import org.mybatis.generator.api.IntrospectedColumn; import org.mybatis.generator.api.IntrospectedTable; import org.mybatis.generator.api.dom.java.CompilationUnit; import org.mybatis.generator.api.dom.java.…...
2024/4/13 8:24:07 - 震惊!某专家道出Java中的值传递与引用传递居然......
值传递与引用传递实质就是方法操作在内存中是自己单开了一个空间自己玩自己的,还是在对象的空间中陪对象一起玩这样一个问题,废话不多说,直接上代码,具体的内容均在注释中. public class Test { //定义一个Test类int i ; //成员变量ivoid change(int i){ //无返回值方法cha…...
2024/4/28 13:03:26 - Java基础篇--反射和注解
目录 前言 Java的反射机制 反射机制的概念 ***:什么场合需要用到反射? Java反射API 反射的步骤 ***:获取Class对象的3种方法 ***:Class.forName()和ClassLoader.loadClass()有什么区别? ***:程序判断题&…...
2024/4/6 9:56:19
最新文章
- 三层交换机与防火墙连通上网实验
防火墙是一种网络安全设备,用于监控和控制网络流量。它可以帮助防止未经授权的访问,保护网络免受攻击和恶意软件感染。防火墙可以根据预定义的规则过滤流量,例如允许或阻止特定IP地址或端口的流量。它也可以检测和阻止恶意软件、病毒和其他威…...
2024/5/9 5:30:32 - 梯度消失和梯度爆炸的一些处理方法
在这里是记录一下梯度消失或梯度爆炸的一些处理技巧。全当学习总结了如有错误还请留言,在此感激不尽。 权重和梯度的更新公式如下: w w − η ⋅ ∇ w w w - \eta \cdot \nabla w ww−η⋅∇w 个人通俗的理解梯度消失就是网络模型在反向求导的时候出…...
2024/5/7 10:36:02 - 第十一届蓝桥杯物联网试题(省赛)
对于通信方面,还是终端A、B都保持接收状态,当要发送的数组不为空再发送数据,发送完后立即清除,接收数据的数组不为空则处理,处理完后立即清除,分工明确 继电器不亮一般可能是电压不够 将数据加空格再加\r…...
2024/5/9 4:40:40 - 实现窗口拖拽移动
import Vue from "vue"; /* * 定义公共js里,在入口文件main.js中import; * 给elementUI的dialog上加上 v-dialogDrag 指令就可以实现弹窗的全屏和拉伸了。 */ // v-dialogDrag: 弹窗拖拽水平方向伸缩 Vue.directive(dialogDrag, { bind(e…...
2024/5/9 4:49:44 - 416. 分割等和子集问题(动态规划)
题目 题解 class Solution:def canPartition(self, nums: List[int]) -> bool:# badcaseif not nums:return True# 不能被2整除if sum(nums) % 2 ! 0:return False# 状态定义:dp[i][j]表示当背包容量为j,用前i个物品是否正好可以将背包填满ÿ…...
2024/5/8 19:32:33 - 【Java】ExcelWriter自适应宽度工具类(支持中文)
工具类 import org.apache.poi.ss.usermodel.Cell; import org.apache.poi.ss.usermodel.CellType; import org.apache.poi.ss.usermodel.Row; import org.apache.poi.ss.usermodel.Sheet;/*** Excel工具类** author xiaoming* date 2023/11/17 10:40*/ public class ExcelUti…...
2024/5/7 22:31:36 - Spring cloud负载均衡@LoadBalanced LoadBalancerClient
LoadBalance vs Ribbon 由于Spring cloud2020之后移除了Ribbon,直接使用Spring Cloud LoadBalancer作为客户端负载均衡组件,我们讨论Spring负载均衡以Spring Cloud2020之后版本为主,学习Spring Cloud LoadBalance,暂不讨论Ribbon…...
2024/5/9 2:44:26 - TSINGSEE青犀AI智能分析+视频监控工业园区周界安全防范方案
一、背景需求分析 在工业产业园、化工园或生产制造园区中,周界防范意义重大,对园区的安全起到重要的作用。常规的安防方式是采用人员巡查,人力投入成本大而且效率低。周界一旦被破坏或入侵,会影响园区人员和资产安全,…...
2024/5/8 20:33:13 - VB.net WebBrowser网页元素抓取分析方法
在用WebBrowser编程实现网页操作自动化时,常要分析网页Html,例如网页在加载数据时,常会显示“系统处理中,请稍候..”,我们需要在数据加载完成后才能继续下一步操作,如何抓取这个信息的网页html元素变化&…...
2024/5/9 3:15:57 - 【Objective-C】Objective-C汇总
方法定义 参考:https://www.yiibai.com/objective_c/objective_c_functions.html Objective-C编程语言中方法定义的一般形式如下 - (return_type) method_name:( argumentType1 )argumentName1 joiningArgument2:( argumentType2 )argumentName2 ... joiningArgu…...
2024/5/7 16:57:02 - 【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5713-洛谷团队系统【入门2分支结构】🌏题目描述🌏输入格…...
2024/5/7 14:58:59 - 【ES6.0】- 扩展运算符(...)
【ES6.0】- 扩展运算符... 文章目录 【ES6.0】- 扩展运算符...一、概述二、拷贝数组对象三、合并操作四、参数传递五、数组去重六、字符串转字符数组七、NodeList转数组八、解构变量九、打印日志十、总结 一、概述 **扩展运算符(...)**允许一个表达式在期望多个参数࿰…...
2024/5/8 20:58:56 - 摩根看好的前智能硬件头部品牌双11交易数据极度异常!——是模式创新还是饮鸩止渴?
文 | 螳螂观察 作者 | 李燃 双11狂欢已落下帷幕,各大品牌纷纷晒出优异的成绩单,摩根士丹利投资的智能硬件头部品牌凯迪仕也不例外。然而有爆料称,在自媒体平台发布霸榜各大榜单喜讯的凯迪仕智能锁,多个平台数据都表现出极度异常…...
2024/5/9 1:35:21 - Go语言常用命令详解(二)
文章目录 前言常用命令go bug示例参数说明 go doc示例参数说明 go env示例 go fix示例 go fmt示例 go generate示例 总结写在最后 前言 接着上一篇继续介绍Go语言的常用命令 常用命令 以下是一些常用的Go命令,这些命令可以帮助您在Go开发中进行编译、测试、运行和…...
2024/5/9 4:12:16 - 用欧拉路径判断图同构推出reverse合法性:1116T4
http://cplusoj.com/d/senior/p/SS231116D 假设我们要把 a a a 变成 b b b,我们在 a i a_i ai 和 a i 1 a_{i1} ai1 之间连边, b b b 同理,则 a a a 能变成 b b b 的充要条件是两图 A , B A,B A,B 同构。 必要性显然࿰…...
2024/5/7 16:05:05 - 【NGINX--1】基础知识
1、在 Debian/Ubuntu 上安装 NGINX 在 Debian 或 Ubuntu 机器上安装 NGINX 开源版。 更新已配置源的软件包信息,并安装一些有助于配置官方 NGINX 软件包仓库的软件包: apt-get update apt install -y curl gnupg2 ca-certificates lsb-release debian-…...
2024/5/8 18:06:50 - Hive默认分割符、存储格式与数据压缩
目录 1、Hive默认分割符2、Hive存储格式3、Hive数据压缩 1、Hive默认分割符 Hive创建表时指定的行受限(ROW FORMAT)配置标准HQL为: ... ROW FORMAT DELIMITED FIELDS TERMINATED BY \u0001 COLLECTION ITEMS TERMINATED BY , MAP KEYS TERMI…...
2024/5/8 1:37:32 - 【论文阅读】MAG:一种用于航天器遥测数据中有效异常检测的新方法
文章目录 摘要1 引言2 问题描述3 拟议框架4 所提出方法的细节A.数据预处理B.变量相关分析C.MAG模型D.异常分数 5 实验A.数据集和性能指标B.实验设置与平台C.结果和比较 6 结论 摘要 异常检测是保证航天器稳定性的关键。在航天器运行过程中,传感器和控制器产生大量周…...
2024/5/9 1:42:21 - --max-old-space-size=8192报错
vue项目运行时,如果经常运行慢,崩溃停止服务,报如下错误 FATAL ERROR: CALL_AND_RETRY_LAST Allocation failed - JavaScript heap out of memory 因为在 Node 中,通过JavaScript使用内存时只能使用部分内存(64位系统&…...
2024/5/9 5:02:59 - 基于深度学习的恶意软件检测
恶意软件是指恶意软件犯罪者用来感染个人计算机或整个组织的网络的软件。 它利用目标系统漏洞,例如可以被劫持的合法软件(例如浏览器或 Web 应用程序插件)中的错误。 恶意软件渗透可能会造成灾难性的后果,包括数据被盗、勒索或网…...
2024/5/9 4:31:45 - JS原型对象prototype
让我简单的为大家介绍一下原型对象prototype吧! 使用原型实现方法共享 1.构造函数通过原型分配的函数是所有对象所 共享的。 2.JavaScript 规定,每一个构造函数都有一个 prototype 属性,指向另一个对象,所以我们也称为原型对象…...
2024/5/8 12:44:41 - C++中只能有一个实例的单例类
C中只能有一个实例的单例类 前面讨论的 President 类很不错,但存在一个缺陷:无法禁止通过实例化多个对象来创建多名总统: President One, Two, Three; 由于复制构造函数是私有的,其中每个对象都是不可复制的,但您的目…...
2024/5/8 9:51:44 - python django 小程序图书借阅源码
开发工具: PyCharm,mysql5.7,微信开发者工具 技术说明: python django html 小程序 功能介绍: 用户端: 登录注册(含授权登录) 首页显示搜索图书,轮播图࿰…...
2024/5/8 1:37:29 - 电子学会C/C++编程等级考试2022年03月(一级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:双精度浮点数的输入输出 输入一个双精度浮点数,保留8位小数,输出这个浮点数。 时间限制:1000 内存限制:65536输入 只有一行,一个双精度浮点数。输出 一行,保留8位小数的浮点数。样例输入 3.1415926535798932样例输出 3.1…...
2024/5/9 4:33:29 - 配置失败还原请勿关闭计算机,电脑开机屏幕上面显示,配置失败还原更改 请勿关闭计算机 开不了机 这个问题怎么办...
解析如下:1、长按电脑电源键直至关机,然后再按一次电源健重启电脑,按F8健进入安全模式2、安全模式下进入Windows系统桌面后,按住“winR”打开运行窗口,输入“services.msc”打开服务设置3、在服务界面,选中…...
2022/11/19 21:17:18 - 错误使用 reshape要执行 RESHAPE,请勿更改元素数目。
%读入6幅图像(每一幅图像的大小是564*564) f1 imread(WashingtonDC_Band1_564.tif); subplot(3,2,1),imshow(f1); f2 imread(WashingtonDC_Band2_564.tif); subplot(3,2,2),imshow(f2); f3 imread(WashingtonDC_Band3_564.tif); subplot(3,2,3),imsho…...
2022/11/19 21:17:16 - 配置 已完成 请勿关闭计算机,win7系统关机提示“配置Windows Update已完成30%请勿关闭计算机...
win7系统关机提示“配置Windows Update已完成30%请勿关闭计算机”问题的解决方法在win7系统关机时如果有升级系统的或者其他需要会直接进入一个 等待界面,在等待界面中我们需要等待操作结束才能关机,虽然这比较麻烦,但是对系统进行配置和升级…...
2022/11/19 21:17:15 - 台式电脑显示配置100%请勿关闭计算机,“准备配置windows 请勿关闭计算机”的解决方法...
有不少用户在重装Win7系统或更新系统后会遇到“准备配置windows,请勿关闭计算机”的提示,要过很久才能进入系统,有的用户甚至几个小时也无法进入,下面就教大家这个问题的解决方法。第一种方法:我们首先在左下角的“开始…...
2022/11/19 21:17:14 - win7 正在配置 请勿关闭计算机,怎么办Win7开机显示正在配置Windows Update请勿关机...
置信有很多用户都跟小编一样遇到过这样的问题,电脑时发现开机屏幕显现“正在配置Windows Update,请勿关机”(如下图所示),而且还需求等大约5分钟才干进入系统。这是怎样回事呢?一切都是正常操作的,为什么开时机呈现“正…...
2022/11/19 21:17:13 - 准备配置windows 请勿关闭计算机 蓝屏,Win7开机总是出现提示“配置Windows请勿关机”...
Win7系统开机启动时总是出现“配置Windows请勿关机”的提示,没过几秒后电脑自动重启,每次开机都这样无法进入系统,此时碰到这种现象的用户就可以使用以下5种方法解决问题。方法一:开机按下F8,在出现的Windows高级启动选…...
2022/11/19 21:17:12 - 准备windows请勿关闭计算机要多久,windows10系统提示正在准备windows请勿关闭计算机怎么办...
有不少windows10系统用户反映说碰到这样一个情况,就是电脑提示正在准备windows请勿关闭计算机,碰到这样的问题该怎么解决呢,现在小编就给大家分享一下windows10系统提示正在准备windows请勿关闭计算机的具体第一种方法:1、2、依次…...
2022/11/19 21:17:11 - 配置 已完成 请勿关闭计算机,win7系统关机提示“配置Windows Update已完成30%请勿关闭计算机”的解决方法...
今天和大家分享一下win7系统重装了Win7旗舰版系统后,每次关机的时候桌面上都会显示一个“配置Windows Update的界面,提示请勿关闭计算机”,每次停留好几分钟才能正常关机,导致什么情况引起的呢?出现配置Windows Update…...
2022/11/19 21:17:10 - 电脑桌面一直是清理请关闭计算机,windows7一直卡在清理 请勿关闭计算机-win7清理请勿关机,win7配置更新35%不动...
只能是等着,别无他法。说是卡着如果你看硬盘灯应该在读写。如果从 Win 10 无法正常回滚,只能是考虑备份数据后重装系统了。解决来方案一:管理员运行cmd:net stop WuAuServcd %windir%ren SoftwareDistribution SDoldnet start WuA…...
2022/11/19 21:17:09 - 计算机配置更新不起,电脑提示“配置Windows Update请勿关闭计算机”怎么办?
原标题:电脑提示“配置Windows Update请勿关闭计算机”怎么办?win7系统中在开机与关闭的时候总是显示“配置windows update请勿关闭计算机”相信有不少朋友都曾遇到过一次两次还能忍但经常遇到就叫人感到心烦了遇到这种问题怎么办呢?一般的方…...
2022/11/19 21:17:08 - 计算机正在配置无法关机,关机提示 windows7 正在配置windows 请勿关闭计算机 ,然后等了一晚上也没有关掉。现在电脑无法正常关机...
关机提示 windows7 正在配置windows 请勿关闭计算机 ,然后等了一晚上也没有关掉。现在电脑无法正常关机以下文字资料是由(历史新知网www.lishixinzhi.com)小编为大家搜集整理后发布的内容,让我们赶快一起来看一下吧!关机提示 windows7 正在配…...
2022/11/19 21:17:05 - 钉钉提示请勿通过开发者调试模式_钉钉请勿通过开发者调试模式是真的吗好不好用...
钉钉请勿通过开发者调试模式是真的吗好不好用 更新时间:2020-04-20 22:24:19 浏览次数:729次 区域: 南阳 > 卧龙 列举网提醒您:为保障您的权益,请不要提前支付任何费用! 虚拟位置外设器!!轨迹模拟&虚拟位置外设神器 专业用于:钉钉,外勤365,红圈通,企业微信和…...
2022/11/19 21:17:05 - 配置失败还原请勿关闭计算机怎么办,win7系统出现“配置windows update失败 还原更改 请勿关闭计算机”,长时间没反应,无法进入系统的解决方案...
前几天班里有位学生电脑(windows 7系统)出问题了,具体表现是开机时一直停留在“配置windows update失败 还原更改 请勿关闭计算机”这个界面,长时间没反应,无法进入系统。这个问题原来帮其他同学也解决过,网上搜了不少资料&#x…...
2022/11/19 21:17:04 - 一个电脑无法关闭计算机你应该怎么办,电脑显示“清理请勿关闭计算机”怎么办?...
本文为你提供了3个有效解决电脑显示“清理请勿关闭计算机”问题的方法,并在最后教给你1种保护系统安全的好方法,一起来看看!电脑出现“清理请勿关闭计算机”在Windows 7(SP1)和Windows Server 2008 R2 SP1中,添加了1个新功能在“磁…...
2022/11/19 21:17:03 - 请勿关闭计算机还原更改要多久,电脑显示:配置windows更新失败,正在还原更改,请勿关闭计算机怎么办...
许多用户在长期不使用电脑的时候,开启电脑发现电脑显示:配置windows更新失败,正在还原更改,请勿关闭计算机。。.这要怎么办呢?下面小编就带着大家一起看看吧!如果能够正常进入系统,建议您暂时移…...
2022/11/19 21:17:02 - 还原更改请勿关闭计算机 要多久,配置windows update失败 还原更改 请勿关闭计算机,电脑开机后一直显示以...
配置windows update失败 还原更改 请勿关闭计算机,电脑开机后一直显示以以下文字资料是由(历史新知网www.lishixinzhi.com)小编为大家搜集整理后发布的内容,让我们赶快一起来看一下吧!配置windows update失败 还原更改 请勿关闭计算机&#x…...
2022/11/19 21:17:01 - 电脑配置中请勿关闭计算机怎么办,准备配置windows请勿关闭计算机一直显示怎么办【图解】...
不知道大家有没有遇到过这样的一个问题,就是我们的win7系统在关机的时候,总是喜欢显示“准备配置windows,请勿关机”这样的一个页面,没有什么大碍,但是如果一直等着的话就要两个小时甚至更久都关不了机,非常…...
2022/11/19 21:17:00 - 正在准备配置请勿关闭计算机,正在准备配置windows请勿关闭计算机时间长了解决教程...
当电脑出现正在准备配置windows请勿关闭计算机时,一般是您正对windows进行升级,但是这个要是长时间没有反应,我们不能再傻等下去了。可能是电脑出了别的问题了,来看看教程的说法。正在准备配置windows请勿关闭计算机时间长了方法一…...
2022/11/19 21:16:59 - 配置失败还原请勿关闭计算机,配置Windows Update失败,还原更改请勿关闭计算机...
我们使用电脑的过程中有时会遇到这种情况,当我们打开电脑之后,发现一直停留在一个界面:“配置Windows Update失败,还原更改请勿关闭计算机”,等了许久还是无法进入系统。如果我们遇到此类问题应该如何解决呢࿰…...
2022/11/19 21:16:58 - 如何在iPhone上关闭“请勿打扰”
Apple’s “Do Not Disturb While Driving” is a potentially lifesaving iPhone feature, but it doesn’t always turn on automatically at the appropriate time. For example, you might be a passenger in a moving car, but your iPhone may think you’re the one dri…...
2022/11/19 21:16:57
