\(Tips:\)本文数学公式较多(可能我写的烂)，加载较慢耐心等待，如有[Math Process Error]的情况请刷新。

该来的还是要来qwq

现在的题真Duliu，\(10\)道题\(9\)个是\(FFT/NTT\)，还有一个\(FWT\)。

最近做题遇到一堆要优化到\(nlog_2n\)，没办法只能学了。。

写一篇 自己都看不懂的 \(blog\)加深理解

---

\(Easy-1.FFT\)

定义

• FFT\((Fast\ Fourier\ Transformation)\)

  中文名称：快速傅里叶离散变换

  (Fake Funny TLE)

---

\(Q:\)这个东西是用来干什么的呢？

\(A:\)想必大家都知道\(FFT\)可以快速求高精乘法吧。

利用\(FFT\)可以做到在\(O(nlog_2n)\)的复杂度内快速求出两个多项式/卷积相乘的结果

• 多项式

  对于一个形如

  \[A(x)=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots+a_0x^0=\sum_{i=0}^{n-1}a_ix^i\]

  的式子，称其为一个多项式。其中最大的次数称为多项式的次数。

  • 系数表示

    将\(n-1\)次多项式的系数看做一个\(n\)维向量：

    \[\vec a=(a_0,a_1,\dots,a_{n-1})\]

    即为多项式的系数表示

  • 点值表示

    对于一个\(n-1\)次多项式\(A(x)\)，将\(n\)的不相同的\(x\)代入得到一系列点\(\{(x_0,y_0)\dots\}\)，可以唯一确定多项式\(A(x)\)

  • 多项式乘法

    对于两个多项式\(A(x),B(x)\)

    \[A(x)=\sum_{i=0}^{n-1}a_ix^i,B(x)=\sum_{i=0}^{n-1}b_ix^i\]

    有\(C(x)=A(x)* B(x)\)

    \[C(x)=\sum_{i=0}^{2n-2}\sum_{j+k=i}a_jb_kx^i\]

  ---

• 卷积

  对于两个向量\(\vec a=(a_0,a_1,\dots,a_{n-1}),\vec b=(b_0,b_1,\dots,b_{n-1})\)

  有卷积\(\vec a\otimes\vec b=c(c_0,c_1,\dots,c_{2n-2})\)

  其中有\(c_k=\sum_{i,j}^{i+j=k}\limits a_ib_j\)

  和上面多项式乘法非常类似。

---

那么如何计算多项式乘法呢？

一个显然的做法是按照定义\(O(n^2)\)计算。

不过我们发现，对于两个点值表示\(\{(ax_0,ay_0),\dots\},\{(bx_0,by_0),\dots\}\)，可以\(O(n)\)地相乘得到\(C(x)\)的点值表达式。

那么有没有什么方法可以快速的将多项式转成点值表示和逆回来呢？

有的有的，请留下您的邮箱 \(FFT\)就可以做到这一点。

\(FFT\)大概包含\(3\)个步骤：

Part1

多项式 \(\Rightarrow\) 点值表示 （\(DFT,O(nlog_2n)\)）

Part2

点值表示相乘 （\(O(n)\)）

Part3

点值表示 \(\Rightarrow\) 多项式 （\(IDFT,O(nlog_2n)\)）

---

Prepare

• 复数

  复数由实部和虚部组成，例如\(2+3i\)（其中\(i\)为虚数单位，\(i^2=\sqrt{-1}\)）。可以把它理解为一个点或向量\((2,3)\)。

  复数运算法则：

  • 加法

    实部虚部分别相加

    \((2+3i)+(3+3i)=(5+6i)\)

    

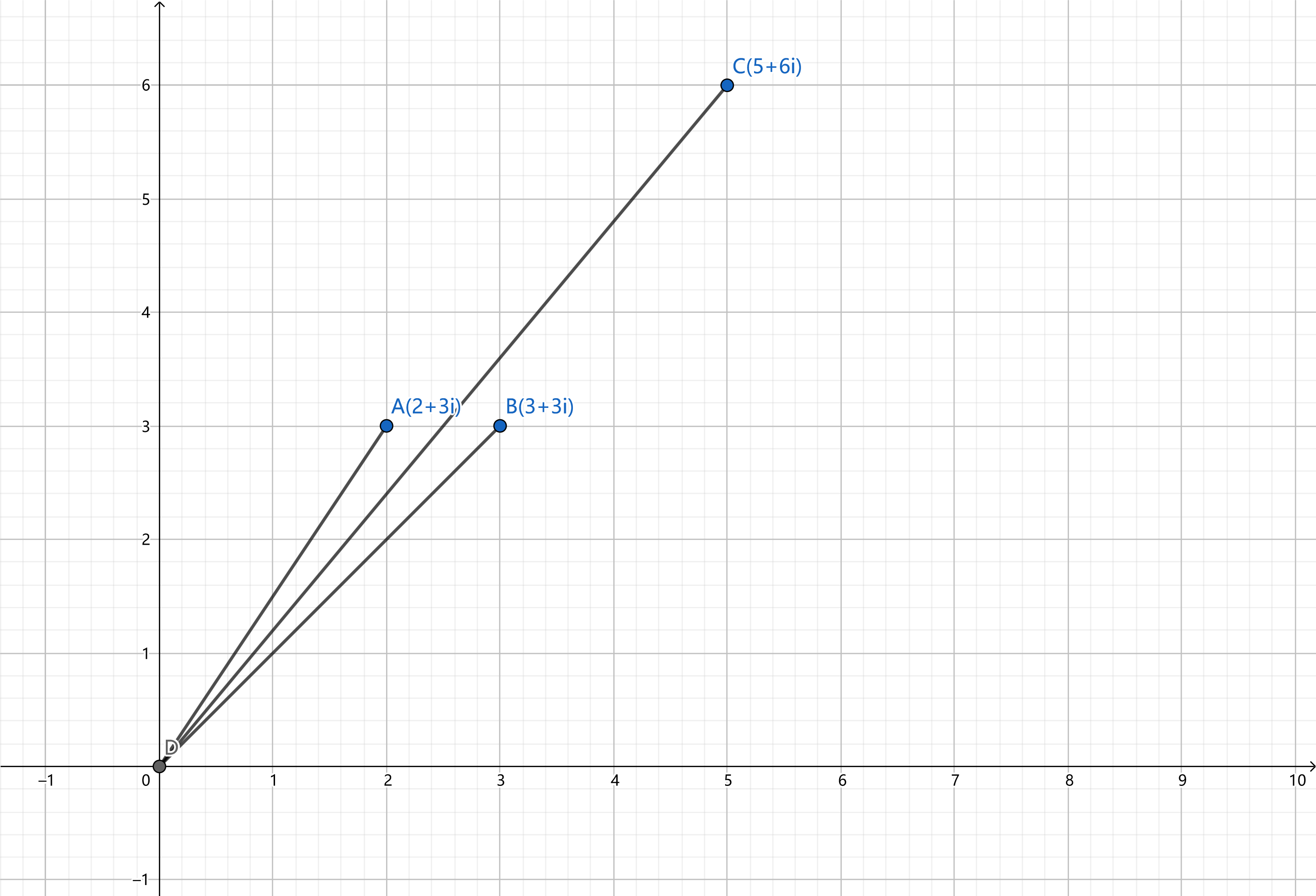
  • 乘法

    类似多项式乘法，在坐标系中直观表现为模长相乘，幅角相加（幅角为\(x\)轴逆时针转动的角度）。

    \((2+3i)* (3+3i)=6+6i+9i+9i^2=(-3+15i)\)

    

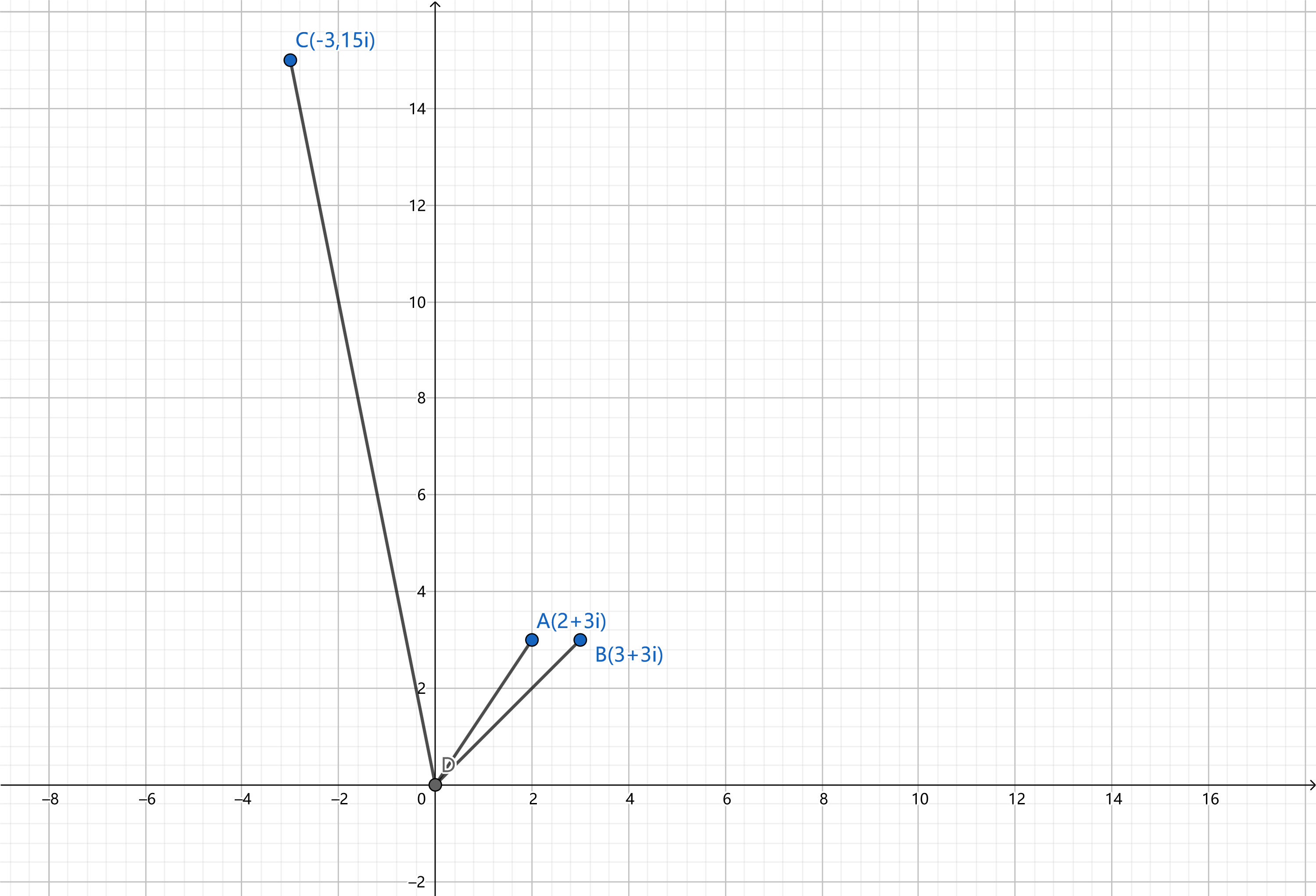
  • 除法

    类似分数的化简

    \(\frac{2+3i}{3+3i}=\frac{(2+3i)* (3-3i)}{(3+3i)* (3-3i)}=\frac{6-6i+9i-9i^2}{9-9i^2}=\frac{15+3i}{18}=\frac{15}{18}+\frac{3i}{18}\)

    图就不画了，太麻烦了。

---

• 思想

  规定点值表示中的\(n\)个\(x\)值为\(n\)个模长为\(1\)的复数。

但是并不是随机的复数，是均匀分布在单位圆（以原点为圆心，半径为\(1\)）上的\(n\)个复数，将圆\(n\)等分。

将点从\(0\)开始标号，设第\(0\)个点为\(\omega_n^0\)（和我一起读，\(Omega\sim\)），以此类推。

以\((1,0)\)为起点，由复数乘法规则得：\(\omega_n^i\)的模长一定是\(1\)。

则\(\omega_n^i\)对应的点为\((\cos(\frac{i}{n}2\pi),\sin(\frac{i}{n}2\pi))\)。（采用弧度制）

把这些复数称为\(n\)次单位根。

接下来进入正题。

---

DFT (Discrete Fourier Transform)

\(Q:\)学了这么多，但是复杂度不还是\(O(n^2)\)吗？

\(A:\)下面就介绍\(O(nlog_2n)\)的算法。

• \(Cooley-Tukey\)算法

  发明者：\(J.\ W.\ Cooley\&J.\ W.\ Tukey\)

  思想：分治

使\(n=2^m(m\in \mathbb{Z})\)，若不够高位用\(0\)补齐（显然没有影响）。

接着，对于多项式\(A(x)=\sum_{i=0}^{n-1}\limits a_ix^i\)，将其各项按次数奇偶性分类：

\[A(x)=(a_0x^0+a_2x^2+\dots+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+\dots+a_{n-1}x^{n-1})\]

现在设：

\[A_1(x)=(a_0x^0+a_2x^1+\dots+a_{n-2}x^{\frac{n-2}2})\]

\[A_2(x)=(a_1x^0+a_3x^1+\dots+a_{n-1}x^{\frac{n-2}2})\]

则有：

\[A(x)=A_1(x^2)+xA_2(x^2)\]

对于\(k<\frac n2,\)有：

\[A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\]

\[=A_1(\omega_{\frac n2}^k)+\omega_n^kA_2(\omega_{\frac n2}^k)\]

同理，对于\(k+\frac n2\)有：

\[A(\omega_n^{k+\frac n2})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac n2}A_2(\omega_n^{2k+n})\]

\[=A_1(\omega_{\frac n2}^k*\omega_n^n)+\omega_n^k*\omega_n^{\frac n2}A_2(\omega_{\frac n2}^k*\omega_n^n)\]

因为\(\omega_n^{\frac n2},\omega_n^n\) 分别对于着\((-1,0),(1,0)\)，则

\[A(\omega_n^{k+\frac n2})=A_1(\omega_{\frac n2}^k)-\omega_n^kA_2(\omega_{\frac n2}^k)\]

于是，问题被分成了更小的子问题，递归求解即可。

时间复杂度？这不某年初赛题吗 \(T(n)=2T(\frac n2)+O(n)=O(nlog_2n)\)

---

IDFT (Inverse Discrete Fourier Transform)

\(Q:\)既然把多项式变成了点值表示，那么怎么把它变回去呢？？

首先，这个问题相当于解一个线性方程组：

\[\begin{cases}a_0(\omega_n^0)^0\quad+a_1(\omega_n^0)^1\quad+\cdots+a_{n-1}(\omega_n^0)^{n-1}\quad=A(\omega_n^0)\\a_0(\omega_n^1)^0\quad+a_1(\omega_n^1)^1\quad+\cdots+a_{n-1}(\omega_n^1)^{n-1}\quad=A(\omega_n^1)\\\qquad\vdots\qquad\qquad\vdots\qquad\qquad\ddots\qquad\qquad\vdots\qquad\qquad\qquad\vdots\\a_0(\omega_n^{n-1})^0+a_1(\omega_n^{n-1})^1+\cdots+a_{n-1}(\omega_n^{n-1})^{n-1}=A(\omega_n^{n-1})\end{cases}\]

写成矩阵：

\[\begin{bmatrix}(\omega_n^0)^0&(\omega_n^0)^1&\cdots&(\omega_n^0)^{n-1}\\(\omega_n^1)^0&(\omega_n^1)^1&\cdots&(\omega_n^1)^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\cdots&(\omega_n^{n-1})\end{bmatrix}\begin{bmatrix}a_0\\a_1\\\vdots\\a_{n-1}\end{bmatrix}=\begin{bmatrix}A(\omega_n^0)\\A(\omega_n^1)\\\vdots \\A(\omega_n^{n-1})\\\end{bmatrix}\]

求解矩阵逆我会，高斯消元

\(O(n^3)\)是不可能的，这辈子都不可能的。

设上面式子中左边矩阵为\(X\)

现在考虑矩阵\(Y,Y_{i,j}=(\omega_n^{-i})^j,Z=X* Y\)

则：

\[Y=\begin{bmatrix}(\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\(\omega_n^{-1})^0&(\omega_n^{-1})^1&\cdots&(\omega_n^{-1})^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})\end{bmatrix}\]

\[Z_{i,j}=\sum_{k=0}^{n-1}X_{i,k}Y_{k,j}\]

\[=\sum_{k=0}^{n-1}\omega_n^{ik}\omega_n^{-jk}\]

\[=\sum_{k=0}^{n-1}\omega_n^{k(j-i)}\]

那么当\(i=j\)时

\[Z_{i,j}=n\omega_n^0=n\]

否则当\(i\not=j\)时

由等比数列求和公式：

\[Z_{i,j}=\frac{a_1-a_n* q}{1-q}\]

\[=\frac{\omega_n^0-\omega_n^{(n-1)* (j-i)}* \omega_n^{j-i}}{1-\omega_n^{j-i}}\]

\[=\frac{1-\omega_n^{n* (j-i)}}{1-\omega_n^{j-i}}\]

\[=\frac{1-1}{1-\omega_n^{j-i}}\]

\[=0\]

那么就得到

\[X* Y=nI\]

（\(I\)指单位矩阵）

\[X* \frac 1nY=I\]

\[X^{-1}=\frac 1nY\]

也就是说，我们只要把\(DFT\)过程中的点值选取\(\omega_n^i\)换成\(\omega_n^{-i}\)，进行一次\(DFT\)后把结果除以\(n\)就可以了。

时间复杂度证明同上。

那么这就是\(FFT\)的过程了。

是不是很简单啊。

---

代码实现

首先是最基本的\(FFT\)。

采用简单的递归实现。

时间复杂度 \(O(nlog_2n)\)

空间复杂度 \(O(nlog_2n)\)

代码：

#include <cmath>
#include <cstdio>struct Complex//自定义复数，STL太慢
{double x,y;//x为实部，y为虚部inline Complex operator+(const Complex &a)//加法{return (Complex){x+a.x,y+a.y};}inline Complex operator-(const Complex &a)//减法{return (Complex){x-a.x,y-a.y};}inline Complex operator*(const Complex &a)//乘法{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}//除法用不到就没写
}Pol[100005],Tmp[100005],Ome[100005],Inv[100005];
//Pol - 多项式 Tmp - 备用数组 Ome - 预处理\omega_n^i Inv - Ome的逆int n;//n=2^m
const double PI=acos(-1);void Pre()
{for(int i=0;i<n;++i){Ome[i]=(Complex){cos(2.0*PI*i/n), sin(2.0*PI*i/n)};Inv[i]=(Complex){cos(2.0*PI*i/n),-sin(2.0*PI*i/n)};}//简单的预处理
}void FFT(int Siz,int Lef,int Len)//Siz - 子问题大小 Lef - 区域最左端 Len - 步长(a0与a1的距离)
{if(Siz==1)return;int NSiz=Siz>>1;//下一个子问题FFT(NSiz,Lef,Len<<1),FFT(NSiz,Lef+NSiz,Len<<1);//递归处理for(int i=0;i<NSiz;++i){int Pos=Len*i<<1;Tmp[i]=Pol[Lef+Pos]+Ome[i*Len]*Pol[Lef+Pos+Len];//按照定义计算Tmp[i+NSiz]=Pol[Lef+Pos]-Ome[i*Len]*Pol[Lef+Pos+Len];}for(int i=0;i<Siz;++i)Pol[Lef+i*Len]=Tmp[i];//计算完毕
}int main(){Pre();FFT(n=65536,0,1);};

如果是\(IDFT\)把\(FFT\)中\(Ome\)改成\(Inv\)最后结果\(/n\)即可。

---

但是。。这个程序常数太大了！！（自带O(Inf)大常数）

我们来尝试优化程序。

非递归实现

发现，第一层递归将下标二进制中最后一位相同的元素分在了一起。（按奇偶性分类）

第二层将最后两位相同的分在了一起。

于是，同一组数二进制反转后是一段连续的区间（前几位相同，后几位包含所有情况）。

发现，\(i\)最后所在的位置是\(R_i\)(\(i\)的二进制反转)

先把所有数放到最后的位置上，最后向上合并即可。

时间复杂度 \(O(nlog_2n)\)

空间复杂度 \(O(nlog_2n)\)

代码：

#include <cmath>
#include <cstdio>
#include <algorithm>struct Complex//自定义复数，STL太慢
{double x,y;//x为实部，y为虚部inline Complex operator+(const Complex &a)//加法{return (Complex){x+a.x,y+a.y};}inline Complex operator-(const Complex &a)//减法{return (Complex){x-a.x,y-a.y};}inline Complex operator*(const Complex &a)//乘法{return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}//除法用不到就没写
}Pol[100005],Ome[100005],Inv[100005];
//Pol - 多项式 Ome - 预处理\omega_n^i Inv - Ome的逆int n;//n=2^m
const double PI=acos(-1);void Pre()
{for(int i=0;i<n;++i){Ome[i]=(Complex){cos(2.0*PI*i/n), sin(2.0*PI*i/n)};Inv[i]=(Complex){cos(2.0*PI*i/n),-sin(2.0*PI*i/n)};}//简单的预处理
}void FFT(Complex op[])
{for(int i=0,j=0;i<n;++i){if(i>j)std::swap(Pol[i],Pol[j]);//避免重复交换for(int l=n>>1;(j^=l)<l;l>>=1);//反向二进制加法}for(int i=2;i<=n;i<<=1)//现在处理的区间长度（从下往上）{int m=i>>1;//区间子问题for(int j=0;j<n;j+=i)//对每一个区间计算一边for(int k=0;k<m;++k)//此区间的左边(k<i/2){Complex Tmp=op[n/i*k]*Pol[j+k+m];//避免额外内存开销（蝴蝶操作）Pol[j+k+m]=Pol[j+k]-Tmp;Pol[j+k]=Pol[j+k]+Tmp;}}
}int main(){n=65536;Pre();FFT(Ome);FFT(Inv);};

---

P3803 【模板】多项式乘法（FFT）

\(En,\)模板题。

因为乘起来有\(n+m\)次，要补足\(n+m\)。

时间复杂度 \(O(nlog_2n)\)

空间复杂度 \(O(nlog_2n)\)

代码：

#include <cmath>
#include <cstdio>
#include <cctype>
#include <algorithm>char File[1000005],*p1=File,*p2=File;inline char Getchar()
{return p1==p2&&(p2=(p1=File)+fread(File,1,1000000,stdin),p1==p2)?EOF:*p1++;
}inline int Getint()
{register int x=0,c;while(!isdigit(c=Getchar()));for(;isdigit(c);c=Getchar())x=x*10+(c^48);return x;
}struct Complex
{double x,y;inline Complex operator+(const Complex &a){return (Complex){x+a.x,y+a.y};}inline Complex operator-(const Complex &a){return (Complex){x-a.x,y-a.y};}inline Complex operator*(const Complex &a){return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
}a[3000005],b[3000005],Ome[3000005],Inv[3000005];int n,m,Maxl;
const double PI=acos(-1);void Pre()
{for(register int i=0;i<n;++i){Ome[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*i/n)};Inv[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*-i/n)};}
}void FFT(Complex Pol[],Complex op[])
{for(int i=0,j=0;i<n;++i){if(i>j)std::swap(Pol[i],Pol[j]);for(int l=n>>1;(j^=l)<l;l>>=1);}for(register int i=2;i<=n;i<<=1){int m=i>>1;for(register int j=0;j<n;j+=i)for(register int k=0;k<m;++k){Complex Tmp=op[n/i*k]*Pol[j+k+m];Pol[j+k+m]=Pol[j+k]-Tmp;Pol[j+k]=Pol[j+k]+Tmp;}}
}int main()
{n=Getint(),m=Getint();for(register int i=0;i<=n;++i)a[i].x=Getint();for(register int i=0;i<=m;++i)b[i].x=Getint();for(Maxl=n+m,n=2;n<=Maxl;n<<=1);Pre();FFT(a,Ome),FFT(b,Ome);for(int i=0;i<n;++i)a[i]=a[i]*b[i];FFT(a,Inv);for(int i=0;i<=Maxl;++i)printf("%d%c",(int)floor(a[i].x/n+0.5),i==Maxl?'\n':' ');return 0;
}

【模板】A*B Problem升级版（FFT快速傅里叶）

~~我终于会写A*B了！！~~

把\(x\)看成\(10\)多项式乘法即可。

代码：

#include <cmath>
#include <cstdio>
#include <cctype>
#include <algorithm>char File[1000005],*p1=File,*p2=File;inline int Getint()
{register int c;while(!isdigit(c=getchar()));return c^48;
}struct Complex
{double x,y;inline Complex operator+(const Complex &a){return (Complex){x+a.x,y+a.y};}inline Complex operator-(const Complex &a){return (Complex){x-a.x,y-a.y};}inline Complex operator*(const Complex &a){return (Complex){x*a.x-y*a.y,x*a.y+y*a.x};}
}a[150005],b[150005],Ome[150005],Inv[150005];int n,Maxl,s[150005];
const double PI=acos(-1);void Pre()
{for(register int i=0;i<n;++i){Ome[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*i/n)};Inv[i]=(Complex){cos(2.0*PI*i/n),sin(2.0*PI*-i/n)};}
}void FFT(Complex Pol[],Complex op[])
{for(int i=0,j=0;i<n;++i){if(i>j)std::swap(Pol[i],Pol[j]);for(int l=n>>1;(j^=l)<l;l>>=1);}for(register int i=2;i<=n;i<<=1){int m=i>>1;for(register int j=0;j<n;j+=i)for(register int k=0;k<m;++k){Complex Tmp=op[n/i*k]*Pol[j+k+m];Pol[j+k+m]=Pol[j+k]-Tmp;Pol[j+k]=Pol[j+k]+Tmp;}}
}int main()
{scanf("%d",&n),--n;for(register int i=n;i>=0;--i)a[i].x=Getint();for(register int i=n;i>=0;--i)b[i].x=Getint();for(Maxl=n<<1,n=2;n<=Maxl;n<<=1);Pre();FFT(a,Ome),FFT(b,Ome);for(int i=0;i<n;++i)a[i]=a[i]*b[i];FFT(a,Inv);for(int i=0;i<=Maxl+5;++i){s[i]+=(int)floor(a[i].x/n+0.5);s[i+1]+=s[i]/10;s[i]%=10;}bool OK=false;for(int i=Maxl+5;i>=0;--i){if(s[i])OK=true;if(OK||!i)putchar(s[i]^48);}puts("");return 0;
}

---

总结

\(FFT\)太可怕了。。虽然联赛不至于考\((Flag)\)，但是还是很有用的，巩固一下。

参考资料：（\(Dalao\ Orz\)）

从多项式乘法到快速傅里叶变换-Miskcoo

小学生都能看懂的FFT！！！-胡小兔

---

\(2.Medium-NTT(FNT)\)

定义

• NTT\((Number\ Theoretic\ Transforms)\)

  (也称为\(Fast\ Number-Theoretic\ Transform\)，简称\(FNT\))

  中文名称：快速数论变换

  (Not True Transforms)

---

\(Q:FFT\)懂了，\(NTT\)又有什么用呢？\(FFT\)已经够用了啊？？

\(A:\)别急，相对于\(FFT\)来说，\(NTT\)具有更强的针对性，\(NTT\)可以在取模意义下进行多项式乘法计算，从而避免\(FFT\)的\(double\)失精的情况，但\(NTT\)对模数有特殊要求，这在下面会提到。

那么\(NTT\)是怎么实现的呢？

其实\(NTT\)的实现方法与\(FFT\)几乎无异，只需把复数运算换成取模运算即可。

现在来思考为什么\(FFT\)的点值表示要用单位根呢？

因为单位根有如下性质供\(FFT\)利用以加速：

• \(1.\)

\[\omega_n^n=1\]

这一点在\(DFT\)时需要用到

• \(2.\)

所有单位根互不相同，这样才能算出正确答案（例如\(n\)个\(n\)元方程组只有线性无关才有唯一解）。

• \(3.\)

\[\begin{cases} \omega_{2n}^{2k}=\omega_n^k(k<\frac n2)\\ \omega_n^{k+\frac n2}=-\omega_n^k(k\ge\frac n2) \end{cases}\]

显然这样分治才能继续进行

• \(4.\)

\[\sum_{k=0}^{n-1}\omega_n^{k(j-i)}= \begin{cases} 0(i\not=j)\\ n(i=j) \end{cases}\]

这一点\(IDFT\)时有需要。

所以说接下来我们需要找到合适的数满足上面几条性质来代替单位根。

---

• 原根

  设有质数\(p\)，则\(p\)的原根\(g\)满足\(g^k\mod p(1\le k<p-1)\)互不相同。

  那么若质数\(p=q*n+1(n=2^x)\)，则根据费马小定理有\(a^{p-1}\equiv 1(\mod p)\)

  显然，\(g_0\equiv g_{p-1}\equiv 1(\mod p)\)

  若设\(\omega_n=g^q\)，则可以得到\(n\)个不相同的数：\(\omega_n^k(0\le k<n)\)

  满足性质2

  并且\(\omega_n^n\equiv g^{p-1}\equiv 1(\mod p)\)

  满足性质1

  那么就可以得到：

  \(\because p=q*n+1=\frac q2*2n+1,\omega_n=g^q\)

  \(\therefore \omega_{2n}=g^{\frac q2}\)

  \(\omega_{2n}^{2k}=g^{\frac q2*2k}=g^{qk}=\omega_n^k\)

  且

  \(\omega_n^{k+\frac n2}\)

  \(=\omega_n^k*\omega_n^{\frac n2}\)

  \(\because (\omega_n^{\frac n2})^2=\omega_n^n=1\)

  \(\therefore \omega_n^{\frac n2}=\pm1\)

  \(\because \omega\)互不相同

  \(\therefore \omega_n^{\frac n2}=-1\)

  \(\therefore \omega_n^{k+\frac n2}=-\omega_n^k\)

  满足性质3

  最后：对于\(\sum_{k=0}^{n-1}\omega_n^{k(j-i)}\)

  若\(i=j\)，则：

  \(\sum_{k=0}^{n-1}\omega_n^{k(j-i)}\)

  \(=n*\omega_n^0\)

  \(=n\)

  若\(i\not=j\)，则有：

  \(\sum_{k=0}^{n-1}\omega_n^{k(j-i)}\)

  \(=\frac{(q^n-1)a_0}{q-1}\)(等比数列求和，此处\(q\)为公比\((\omega_n^{j-i})\)，\(a_0\)为首项\((\omega_n^0)\))

  \(\because q^n-1=\omega_n^{n(j-i)}-1=(\omega_n^n)^{j-i}-1=0\)

  \(\therefore \sum_{k=0}^{n-1}\omega_n^{k(j-i)}=0\)

  综上所述，满足性质4

\(Q:\)什么？原根怎么求？

\(A:\)我怎么知道，百度啊

一般情况下只需要记住\(998244353\)的原根是\(3\)就好\((998244353=119*2^{23}+1)\)，也可以查表：[Miskcoo's Space]FFT用到的各种素数

---

于是，照着上面说的，\(NTT\)的框架就出来了：

把复数运算换成取模即可。

\(Q:n\)不满\(2^{23}\)怎么办？补满太慢。

\(A:\)把\(\omega_n\)换成\(g^{\frac{p-1}{n}}\)即可。

P3803 【模板】多项式乘法（FFT）

\(Q:\)为什么是\(FFT\)模板？

\(A:\)找不到NTT的 因为这题答案不会超过\(998244353\)，那么用来取模就并不会产生影响。

代码：

#include <cstdio>
#include <cctype>
#include <algorithm>char In[1000005],*p1=In,*p2=In;
#define Getchar (p1==p2&&(p2=(p1=In)+fread(In,1,1000000,stdin),p1==p2)?EOF:*p1++)
inline int Getint()
{register int x=0,c;while(!isdigit(c=Getchar));for(;isdigit(c);c=Getchar)x=x*10+(c^48);return x;
}const int p=998244353,g=3;int Pow(int a,int b)
{if(b<0)return Pow(Pow(a,p-2),-b);//逆元int Res=1;for(;b;b>>=1){if(b&1)Res=Res*1LL*a%p;a=a*1LL*a%p;}return Res%p;
}int n,m,Maxl;
int a[2100005],b[2100005];void NTT(int Pol[],int op)//op=1为DFT,-1为IDFT
{for(int i=0,j=0;i<n;++i){if(i>j)std::swap(Pol[i],Pol[j]);for(int l=n>>1;(j^=l)<l;l>>=1);}for(register int i=2;i<=n;i<<=1){int m=i>>1,Rs=Pow(g,op*(p-1)/i);for(register int j=0;j<n;j+=i){int Root=1;for(register int k=0;k<m;++k){int Tmp=Root*1LL*Pol[j+k+m]%p;Root=Root*1LL*Rs%p;//int Root=Pow(Omega,op*(p-1)/n*k)//不预处理单位根，使用秦九韶算法加速Pol[j+k+m]=Pol[j+k]-Tmp;Pol[j+k]=Pol[j+k]+Tmp;Pol[j+k+m]<0?Pol[j+k+m]+=p:0;//减少取模Pol[j+k]>=p?Pol[j+k]-=p:0;}}}
}int main()
{n=Getint(),m=Getint();for(register int i=0;i<=n;++i)a[i]=Getint();for(register int i=0;i<=m;++i)b[i]=Getint();for(Maxl=n+m,n=2;n<=Maxl;n<<=1);NTT(a,1),NTT(b,1);for(int i=0;i<n;++i)a[i]=a[i]*1LL*b[i]%p;NTT(a,-1);int Invn=Pow(n,p-2);for(int i=0;i<=Maxl;++i)printf("%d%c",int(a[i]*1LL*Invn%p),i==n-1?'\n':' ');//答案同样/nreturn 0;
}

相信有了\(FFT\)的基础，\(NTT\)应该很简单。

参考资料：（\(STO\ Dalao\)）

从多项式乘法到快速傅里叶变换-Miskcoo

从傅里叶变换到数论变换-Menci

---

\(3.Hard-MTT\)

定义

[少女施工中]咕了

---

\(4.Extreme-FWT\)

• FWT\((Fast\ Walsh-Hadamard\ Transform)\)

  中文名称：快速沃尔什变换

  (Fast Wrong-Answer Transform)

---

\(Q:\)有完没完了？\(FWT\)又是什么？现在已经能处理任意情况的多项式乘法了，还要这个干什么？

\(A:\)我也不想学啊，根本背不下来

虽然现在我们可以快速求出\(C=A*B,C_k=\sum_{i+j=k}A_i*B_j\)了，但是现在让你求\(C=A\oplus B,C_k=\sum_{i\oplus j=k}A_i*B_j\)，其中\(\oplus\)代表一个位运算符号，如\(|(or),\&(and),\land(xor)\)，你该怎么做呢？

这时就到\(FWT\)登场了。

接下来让我们对于\(FWT\)的\(3\)种形式感性理解分别讨论

---

\(Part1--FWT(or)\)

设\(A_0,A_1\)分别表示长度为\(n=2^x\)的多项式\(A\)的前半部分和后半部分。

首先，给出\(FWT(A)\)的计算方式：

\[ FWT(A)=\begin{cases} (FWT(A_0),FWT(A_0)+FWT(A_1))&(n>1)\\ A&(n=1) \end{cases} \]

其中\((A,B)\)表示两个多项式相连。

那么\(n=1\)是显然是对的，边界嘛。

至于\(n>1\)的情况如何理解？

对于\(A_0\)和\(A_0\)中两个数下标\(or\)起来一点还在\(A_0\)中（二进制下最高位为\(0\)，是前半部分），那么就只对前半部分有贡献。

对于\(A_1\)和\(A_1\)中两个数，同理只对后半部分有贡献。

对于\(A_0\)和\(A_1\)中的两个数，思考\(FWT(A)_k\)的意义，有：

\[FWT(A)_k=\sum_{i|k=k}A_i\]

因为当\(i|k=k,j|k=k\)时，有\((i|j)|k=k\)，满足\(FWT\)的可合并性质。

那么因为\(A_1\)下标二进制最高位为\(1\)，所以\(or\)起来只对后半部分产生贡献。

贡献就是\(A_0\)对\(A_1\)的贡献（\(A_1\)已经贡献过自己了，不用再加）。

那么式子就很明显了。

同时根据\(FWT(A)\)的意义，容易发现\(FWT(A_0+A_1)=FWT(A_0)+FWT(A_1)\)。

接下来证明\(FWT(A|B)=FWT(A)*FWT(B)\)(保证\(or\)卷积答案的正确性，要不然\(FWT\)就没有用了)。

当\(n=1\)时，性质显然成立

当\(n>1\)时，：

\[ \begin{equation} \begin{split} FWT(A|B)=&FWT((A|B)_0,(A|B)_1)\\ &=FWT(A_0|B_0,A_0|B_1+A_1|B_0+A_1|B_1)\\ &=(FWT(A_0|B_0),FWT(A_0|B_0+A_0|B_1+A_1|B_0+A_1|B_1))\\ &=(FWT(A_0)*FWT(B_0),FWT(A_0)*FWT(B_0)+FWT(A_0)*FWT(B_1)\\ &+FWT(A_1)*FWT(B_0)+FWT(A_1)*FWT(B_1))\\ &=(FWT(A_0)*FWT(B_0),(FWT(A_0)+FWT(A_1))*(FWT(B_0)+FWT(B_1)))\\ &=(FWT(A_0)*FWT(B_0),FWT(A_0+A_1)*FWT(B_0+B_1)))\\ &=(FWT(A_0),FWT(A_0+A_1))*(FWT(B_0),FWT(B_0+B_1))\\ &=FWT(A)*FWT(B) \end{split} \end{equation} \]

由数学归纳法得知，此性质成立。

那么\(or\)的\(FWT\)就很好写了~~代码在后面。

\(Part2--FWT(and)\)

\(and\)的\(FWT\)就和\(or\)的很类似了。

因为\(A_0\)和\(A_1\)最高位不同，那么\(and\)后只对\(A_0\)有贡献。

类似\(or\)的，可以得到\(FWT(A)\)的计算方式：

\[ FWT(A)=\begin{cases} (FWT(A_0)+FWT(A_1),FWT(A_1))&(n>0)\\ A(n=0) \end{cases} \]

至于证明就不写了，和\(or\)的类似，写着麻烦。

\(Part3--FWT(xor)\)

最迷的\(xor\)来了

说实话，在网上找了许多\(Blog\)，似乎都没有给出构造方法，那么我也不会啊

你就当是某位神仙找的规律吧

首先是\(FWT(A)\)的计算方式：

\[ FWT(A)=\begin{cases} (FWT(A_0)+FWT(A_1),FWT(A_0)-FWT(A_1))&(n>0)\\ A(n=0) \end{cases} \]

看着都恶心，这怎么构造出来的啊\(QAQ\)

那么根据定义，很容易证明\(FWT(A\pm B)=FWT(A)\pm FWT(B)\)

因为\(FWT\)是一个线性组合，满足以上性质。

然后是\(FWT(A\land B)=FWT(A)*FWT(B)\)

这个也可以用数学归纳法证明，详见参考资料

---

\(Q:\)等等……是不是少了什么？\(FWT\)后怎么变回去呢？

\(A:\)这还不简单接下来的过程就是\(IFWT\)了！

\(Part4--IFWT(or)\)

\(Emm...\)至于\(IFWT\)呢就很简单了，把变换倒过来即可。

(这不是废话吗)

那么对于\(or\)的\(IFWT\)，考虑之前有\(FWT\)的方程：

\[FWT(A)=(FWT(A_0),FWT(A_0)+FWT(A_1))\]

也就是：

\[FWT(A)_0=FWT(A_0),FWT(A)_1=FWT(A_0)+FWT(A_1)\]

\[FWT(A_0)=FWT(A)_0,FWT(A_1)=FWT(A_0)-FWT(A)_1=FWT(A)_0-FWT(A)_1\]

此时定义\(IFWT(A)_0=FWT(A_0),IFWT(A)_1=FWT(A_1)\) ，也就有：

\[ IFWT(A)=\begin{cases} (IFWT(A_0),IFWT(A_0)-IFWT(A_1))&(n>0)\\ A&(n=0) \end{cases} \]

\(En...\)真简单

\(Part5--IFWT(and)\)

类似\(or\)的\(IFWT\)，可以直接得到：

\[ IFWT(A)=\begin{cases} (IFWT(A_0)-IFWT(A_1),IFWT(A_1))&(n>0)\\ A(n=0) \end{cases} \]

过程类似，这里就不多赘述。。

\(Part6--IFWT(xor)\)

\(xor\)的\(IFWT\)出人意料地一样简单。

由定义得：

\[ \begin{cases} FWT(A)_0=FWT(A_0)+FWT(A_1)\\ FWT(A)_1=FWT(A_0)-FWT(A_1) \end{cases} \]

解方程就简单了。

最后有：

\[ IFWT(A)=\begin{cases} (\frac{IFWT(A_0)+IFWT(A_1)}2,\frac{IFWT(A_0)-IFWT(A_1)}2)&(n>0)\\ A&(n=0) \end{cases} \]

终于完了

---

那么接下来就是看图写话看定义写代码过程了：

这里为了节省代码量把\(6\)个函数写一起了（因为框架大致类似）。

P4717 【模板】快速沃尔什变换

代码：

#include <cstdio>
#include <cstring>
typedef long long ll;const int Mod=998244353,Inv2=(Mod+1)>>1;//Inv2 2在mod998244353下的逆元
int n,a[1<<17],b[1<<17],as[1<<17],bs[1<<17];void FWT(int *A,int op,int t)
//op [1/-1][FWT/IFWT]
//t [1,2,3][or/and/xor]
{for(int i=2;i<=n;i<<=1)//i 区间长度for(int j=0,m=i>>1;j<n;j+=i)//j 区间左端 m 区间大小一半for(int k=0;k<m;++k)//k 正在算第几个数if(t==1)A[j+m+k]=((ll)A[j+m+k]+A[j+k]*op+Mod)%Mod;else if(t==2)A[j+k]=((ll)A[j+k]+A[j+m+k]*op+Mod)%Mod;else{int A0=A[j+k],A1=A[j+m+k];A[j+k]=(ll)(A0+A1)*(op==1?1:Inv2)%Mod;A[j+m+k]=(ll)(A0-A1+Mod)*(op==1?1:Inv2)%Mod;}
}int main()
{scanf("%d",&n),n=1<<n;for(int i=0;i<n;++i)scanf("%d",&as[i]);for(int i=0;i<n;++i)scanf("%d",&bs[i]);for(int t=1;t<=3;++t)//分别计算or/and/xor{memcpy(a,as,sizeof(int)*n);memcpy(b,bs,sizeof(int)*n);FWT(a,1,t),FWT(b,1,t);for(int i=0;i<n;++i)a[i]=a[i]*1LL*b[i]%Mod;FWT(a,-1,t);for(int i=0;i<n;++i)printf("%d%c",a[i],i==n-1?'\n':' ');}return 0;
}

代码应该很好懂，就不解释了。

我只能说：\(FWT\)真好背真好写。

参考资料：（\(Dalao\ TQL\)）

FWT快速沃尔什变换学习笔记-小蒟蒻yyb

关于快速沃尔什变换(FWT)的一点学习和思考-ACMLCZH

后记

终于写完了\(MTT\)有空再补吧。。

这应该时我耗时最长的一篇\(blog\)了（目前为止），如有错误请在评论区指出。

学了这么多多项式，感觉收获不错虽然不会用

看了一下好像还有\(FMT\)(快速莫比乌斯变换)，太可怕了吧。。

我大概一辈子也不会碰吧\((Flag)\)。